题目内容
11.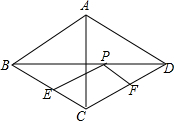 如图,已知菱形ABCD中,对角线AC=12,BD=16,点E、F分别为边BC、CD的中点,点P对角线BD上一动点,则PE+PF的最小值为( )
如图,已知菱形ABCD中,对角线AC=12,BD=16,点E、F分别为边BC、CD的中点,点P对角线BD上一动点,则PE+PF的最小值为( )| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
分析 取AD的中点F′,由菱形的性质可知点F′和F关于BD对称,故此PF=PF′,由两点之间线段最短可知当E、P、F′在一条直线上时,PE+PF有最小值,然后求得EF′的长度即可.
解答 解:取AD的中点F′,连接EF′交BD于点P.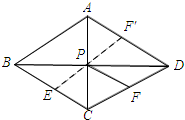
∵四边形ABCD为菱形,
∴AP⊥PB,PA=$\frac{1}{2}AC$,PB=$\frac{1}{2}BD$.
在Rt△ABP中,AB=$\sqrt{A{P}^{2}+P{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
∵ABCD为菱形,E、F′分别是AD、CD的中点,
∴PF=PF′.
∴PE+PF=PE+PF′.
两点之间线段最短可知:当E、P、F′在一条直线上时,PE+PF的最小值.
∵EF=AB,
∴PE+PF的最小值为10.
故选:A.
点评 本题主要考查的是菱形的性质、轴对称--路径最短问题、勾股定理的应用,明确当E、P、F′在一条直线上时PE+PF有最小值是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
20. 如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )
如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )
 如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )
如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )| A. | 35° | B. | 55° | C. | 135° | D. | 125° |
1.若多项式乘法(x+2y)(2x-ky-1)的结果中不含xy项,则k的值为( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
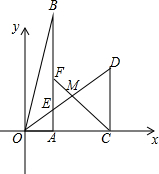 如图,在直角坐标系xOy中,Rt△OAB和Rt△OCD的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,Rt△OAB的面积恒为$\frac{1}{2}$.
如图,在直角坐标系xOy中,Rt△OAB和Rt△OCD的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,Rt△OAB的面积恒为$\frac{1}{2}$.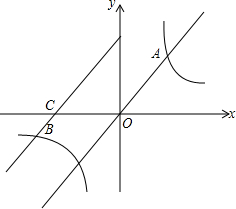 如图,直线y=2x与双曲线y=$\frac{k}{x}$交于点A,将直线y=2x向左平移两个单位后与双曲线y=$\frac{k}{x}$的另一分支交于点B,与x轴交于点C,已知$\frac{BC}{OA}$=$\frac{1}{2}$.那么k=32.
如图,直线y=2x与双曲线y=$\frac{k}{x}$交于点A,将直线y=2x向左平移两个单位后与双曲线y=$\frac{k}{x}$的另一分支交于点B,与x轴交于点C,已知$\frac{BC}{OA}$=$\frac{1}{2}$.那么k=32.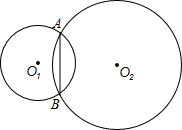 如图,两相交圆的公共弦AB,在⊙O1中为内接正三角形的一边,在⊙O2中为内接正六边形的一边,求这两圆的面积之比.
如图,两相交圆的公共弦AB,在⊙O1中为内接正三角形的一边,在⊙O2中为内接正六边形的一边,求这两圆的面积之比.