题目内容
4.某跳远队准备从甲、乙两名运动员中选去成绩稳定的一名参加比赛,下表是这两名运动员10次测验成绩(单位:m).| 甲 | 5.85 | 5.93 | 6.07 | 5.91 | 5.99 |
| 6.13 | 5.98 | 6.05 | 6.00 | 6.19 | |
| 乙 | 6.11 | 6.08 | 5.83 | 5.92 | 5.84 |
| 5.81 | 6.18 | 6.17 | 5.85 | 6.21 |
分析 根据平均数的计算公式先求出这组数据的平均数,再根据方差公式分别求出甲和乙的方差,然后进行比较,即可得出答案.
解答 解:∵甲的平均数是:$\frac{1}{10}$(5.85+5.93+6.07+5.91+5.99+6.13+5.98+6.05+6.00+6.19)=6,
乙的平均数是:$\frac{1}{10}$(6.11+6.08+5.83+5.92+5.84+5.81+6.18+6.17+5.85+6.21)=6,
∴S甲2=$\frac{1}{10}$[(5.85-6)2+(5.93-6)2+(6.07-6)2+(5.91-6)2+(5.99-6)2+(6.13-6)2+(5.98-6)2+(6.05-6)2+(6.00-6)2+(6.19-6)2]≈0.00954,
S乙2=$\frac{1}{10}$[(6.11-6)2+(6.08-6)2+(5.83-6)2+(5.92-6)2+(5.84-6)2+(5.81-6)2+(6.81-6)2+(6.17-6)2+(5.85-6)2+(6.21-6)2]≈0.02204,
∴S2甲<S2乙,
∴应该选择甲运动员参赛.
点评 本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
15.已知方程2x2-x-3=0的两根为x1,x2,那么$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | -3 |
14.四边形ABCD的对角线相交于O,且AO=BO=CO=DO,则这个四边形( )
| A. | 仅是轴对称图形 | |
| B. | 仅是中心对称图形 | |
| C. | 既是轴对称图形又是中心对称图形 | |
| D. | 既不是轴对称图形,又不是中心对称图形 |
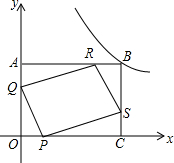 如图,反比例函数y=$\frac{24}{x}$(x>0)的图象经过矩形OABC的顶点B(m+2,m),点P从原点O出发沿线段OC向点C运动,点R从点B出发沿线段BA向点A运动,点P、R速度均为每秒1个单位,点Q从O出发沿折线OA→AB向点B运动,点S从点B出发沿折线BC→CO向点O运动,点Q、S速度均为每秒2个单位,设P、Q、R、S四点同时出发,运动时间为t秒(0<t≤5)
如图,反比例函数y=$\frac{24}{x}$(x>0)的图象经过矩形OABC的顶点B(m+2,m),点P从原点O出发沿线段OC向点C运动,点R从点B出发沿线段BA向点A运动,点P、R速度均为每秒1个单位,点Q从O出发沿折线OA→AB向点B运动,点S从点B出发沿折线BC→CO向点O运动,点Q、S速度均为每秒2个单位,设P、Q、R、S四点同时出发,运动时间为t秒(0<t≤5)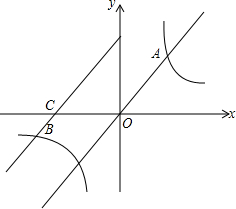 如图,直线y=2x与双曲线y=$\frac{k}{x}$交于点A,将直线y=2x向左平移两个单位后与双曲线y=$\frac{k}{x}$的另一分支交于点B,与x轴交于点C,已知$\frac{BC}{OA}$=$\frac{1}{2}$.那么k=32.
如图,直线y=2x与双曲线y=$\frac{k}{x}$交于点A,将直线y=2x向左平移两个单位后与双曲线y=$\frac{k}{x}$的另一分支交于点B,与x轴交于点C,已知$\frac{BC}{OA}$=$\frac{1}{2}$.那么k=32.