题目内容
5.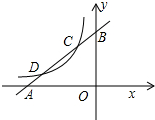 已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线y2=$\frac{k}{x}$(x<0)分别交
已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线y2=$\frac{k}{x}$(x<0)分别交于点C、D,且C点的坐标为(-1,2).
(1)分别求出直线AB及双曲线的解析式;
(2)求出点D的坐标;
(3)利用图象直接写出:当x在什么范围内取值时,y1<y2.
分析 (1)将C(-1,2)分别代入直线y1=x+m与双曲线y2=$\frac{k}{x}$(x<0),用待定系数法求得函数解析式.
(2)把一次函数和反比例函数的解析式联立方程,解方程即可求得;
(4)直线y1=x+m图象在双曲线y2=$\frac{k}{x}$(x<0)下方的部分时x的值,即为y1<y2时x的取值范围.
解答 解:(1)把点C(-1,2)代入y1=x+m,
得:m=3,
∴直线AB的解析式y1=x+3;
把点C(-1,2)代入y2=$\frac{k}{x}$(x<0),
得:k=-2,
∴双曲线的解析式y2=-$\frac{2}{x}$;
(2)解$\left\{\begin{array}{l}{y=x+3}\\{y=-\frac{2}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=1}\end{array}\right.$,
∴D点的坐标为(-2,1);
(3)∵C(-1,2),D的坐标为(-2,1),
观察图形可知:当y1<y2时,x<-2或-1<x<0.
点评 本题考查反比例函数和一次函数解析式的确定.利用数形结合解决取值范围的问题,是非常有效的方法.

练习册系列答案
相关题目
20. 如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )
如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )
 如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )
如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )| A. | 35° | B. | 55° | C. | 135° | D. | 125° |
14.四边形ABCD的对角线相交于O,且AO=BO=CO=DO,则这个四边形( )
| A. | 仅是轴对称图形 | |
| B. | 仅是中心对称图形 | |
| C. | 既是轴对称图形又是中心对称图形 | |
| D. | 既不是轴对称图形,又不是中心对称图形 |
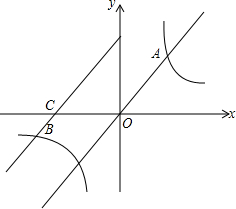 如图,直线y=2x与双曲线y=$\frac{k}{x}$交于点A,将直线y=2x向左平移两个单位后与双曲线y=$\frac{k}{x}$的另一分支交于点B,与x轴交于点C,已知$\frac{BC}{OA}$=$\frac{1}{2}$.那么k=32.
如图,直线y=2x与双曲线y=$\frac{k}{x}$交于点A,将直线y=2x向左平移两个单位后与双曲线y=$\frac{k}{x}$的另一分支交于点B,与x轴交于点C,已知$\frac{BC}{OA}$=$\frac{1}{2}$.那么k=32.
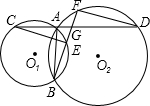 如图:已知⊙O1和⊙O2相交于A、B两点,过A的直线交两圆于C、D两点,过B 的直线交两圆于E、F两点,CD与EF交于点G,连接DF、CE.G为CD的中点.求证:CE=DF.
如图:已知⊙O1和⊙O2相交于A、B两点,过A的直线交两圆于C、D两点,过B 的直线交两圆于E、F两点,CD与EF交于点G,连接DF、CE.G为CD的中点.求证:CE=DF.