题目内容
10. 如图,∠B=∠C,D在BC上,∠BAD=30°,在AC上取AE=AD,∠ADE=∠AED,求∠EDC的度数.
如图,∠B=∠C,D在BC上,∠BAD=30°,在AC上取AE=AD,∠ADE=∠AED,求∠EDC的度数.
分析 设∠EDC=x,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ADE+x=∠B+∠BAD,∠AED=∠C+x,然后整理即可得解.
解答 解:设∠EDC=x,
由三角形的外角性质得,∠ADE+x=∠B+∠BAD,∠AED=∠C+x,
∵∠ADE=∠AED,
∴∠C+x+x=∠B+∠BAD,
∵∠B=∠C,
∴x=$\frac{1}{2}$∠BAD=$\frac{1}{2}$×30°=15°,
即∠EDC=15°.
点评 本题考查了等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记三角形的外角性质列出等式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知方程2x2-x-3=0的两根为x1,x2,那么$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | 3 | D. | -3 |
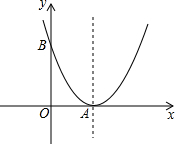 如图,以A为顶点的抛物线与y轴交于点B,已知A,B两点的坐标分别为(3,0)、(0,4).
如图,以A为顶点的抛物线与y轴交于点B,已知A,B两点的坐标分别为(3,0)、(0,4).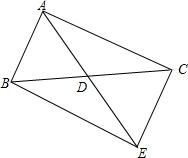 如图,在△ABC中,AD为BC边上的中线,延长AD至E,使DE=AD,连接BE,CE
如图,在△ABC中,AD为BC边上的中线,延长AD至E,使DE=AD,连接BE,CE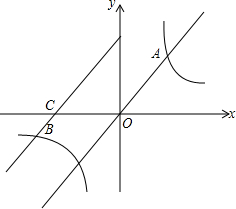 如图,直线y=2x与双曲线y=$\frac{k}{x}$交于点A,将直线y=2x向左平移两个单位后与双曲线y=$\frac{k}{x}$的另一分支交于点B,与x轴交于点C,已知$\frac{BC}{OA}$=$\frac{1}{2}$.那么k=32.
如图,直线y=2x与双曲线y=$\frac{k}{x}$交于点A,将直线y=2x向左平移两个单位后与双曲线y=$\frac{k}{x}$的另一分支交于点B,与x轴交于点C,已知$\frac{BC}{OA}$=$\frac{1}{2}$.那么k=32.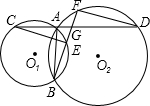 如图:已知⊙O1和⊙O2相交于A、B两点,过A的直线交两圆于C、D两点,过B 的直线交两圆于E、F两点,CD与EF交于点G,连接DF、CE.G为CD的中点.求证:CE=DF.
如图:已知⊙O1和⊙O2相交于A、B两点,过A的直线交两圆于C、D两点,过B 的直线交两圆于E、F两点,CD与EF交于点G,连接DF、CE.G为CD的中点.求证:CE=DF.