题目内容
8.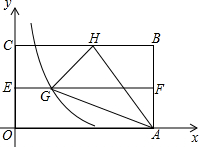 如图,在平面直角坐标系中有矩形OABC,AO=4,点E、F分别是OC和AB的中点,将矩形OABC折叠,使点B落在EF上的点G,折痕为AH,若HG延长线恰好经过点O,反比例函数y=$\frac{k}{x}$的图象过点G,求k的值.
如图,在平面直角坐标系中有矩形OABC,AO=4,点E、F分别是OC和AB的中点,将矩形OABC折叠,使点B落在EF上的点G,折痕为AH,若HG延长线恰好经过点O,反比例函数y=$\frac{k}{x}$的图象过点G,求k的值.
分析 连接OG,过点H作HM⊥x轴于M,交EF于N,则G为OH的中点,N为HM的中点,设BH=a(a>0),AB=b(b>0),则OG=GH=a,AG=AB=b,OM=OA-BH=4-a,通过勾股定理可得出4a2=b2+(4-a)2①和b2=16-a2②,解之即可得出a、b的值,进而即可得出点G的坐标,再根据反比例函数图象上点的坐标特征即可求出k值.
解答 解:如图,连接OG,过点H作HM⊥x轴于M,交EF于N,则G为OH的中点,N为HM的中点.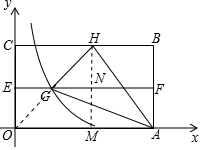
设BH=a(a>0),AB=b(b>0),则OG=GH=a,AG=AB=b,OM=OA-BH=4-a,
在Rt△OMH中,OH=2a,HM=b,OM=4-a,
∴OH2=HM2+OM2,即4a2=b2+(4-a)2①.
在Rt△AOG中,∠AGO=90°,OG=a,AG=b,OA=4,
∴AO2=AG2+OG2,即16=a2+b2,
∴b2=16-a2②.
将②代入①中得:a2+2a-8=0,
解得:a=2或a=-4(舍去),
∴b=$\sqrt{16-{a}^{2}}$=2$\sqrt{3}$,
∴EG=$\frac{1}{2}$OM=1,EO=$\frac{1}{2}$b=$\sqrt{3}$,
∴点G的坐标为(1,$\sqrt{3}$).
∵反比例函数y=$\frac{k}{x}$的图象过点G,
∴k=1×$\sqrt{3}$=$\sqrt{3}$.
点评 本题考查了反比例函数图象上点的坐标特征、矩形的性质、翻折变换、三角形的中位线以及勾股定理,利用勾股定理结合解方程组找出点G的坐标是解题的关键.

练习册系列答案
相关题目
 如图,在⊙O的内接五边形ABCDE中,∠B+∠E=215°,则∠CAD=35°.
如图,在⊙O的内接五边形ABCDE中,∠B+∠E=215°,则∠CAD=35°.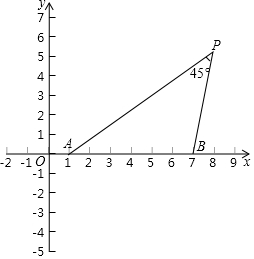 如图,在平面直角坐标系xOy中,点A与点B的坐标分别是(1,0),(7,0).
如图,在平面直角坐标系xOy中,点A与点B的坐标分别是(1,0),(7,0). 如图,平面直角坐标系xOy中,点A是直线y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$上一动点,将点A向右平移1个单位得到点B,点C(1,0),则OB+CB的最小值为$\sqrt{13}$.
如图,平面直角坐标系xOy中,点A是直线y=$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$上一动点,将点A向右平移1个单位得到点B,点C(1,0),则OB+CB的最小值为$\sqrt{13}$.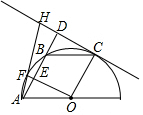 如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作CD∥OF交AB的延长线于点D,延长AF交直线CD于点H.
如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作CD∥OF交AB的延长线于点D,延长AF交直线CD于点H. 如图,在数轴上点A表示的数为$\sqrt{3}$,点B表示的数为6.2,点A、B之间表示整数的点共有( )个.
如图,在数轴上点A表示的数为$\sqrt{3}$,点B表示的数为6.2,点A、B之间表示整数的点共有( )个.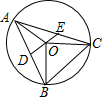 如图,△ABC内接于⊙O,OC⊥OB,OD⊥AB于D交AC于E点,已知⊙O的半径为1,则AE2+CE2的值为( )
如图,△ABC内接于⊙O,OC⊥OB,OD⊥AB于D交AC于E点,已知⊙O的半径为1,则AE2+CE2的值为( )