题目内容
18.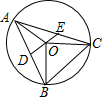 如图,△ABC内接于⊙O,OC⊥OB,OD⊥AB于D交AC于E点,已知⊙O的半径为1,则AE2+CE2的值为( )
如图,△ABC内接于⊙O,OC⊥OB,OD⊥AB于D交AC于E点,已知⊙O的半径为1,则AE2+CE2的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 连接BE,根据垂径定理得到AD=DB,得到EA=EB,∠EAO=∠EBO=∠ACO,根据勾股定理计算即可.
解答 解:连接BE,
∵OD⊥AB,
∴AD=DB,
∴EA=EB,∠EAO=∠EBO=∠ACO,
∵∠ECB+∠EBC=∠ECO+45°+∠EBC=∠OBE+45°+∠EBC=90°,
∴∠BEC=90°,
在直角△BEC中,BE2+CE2=BC2,
∵BC2=2OA2=2,
∴BE2+CE2=2,即AE2+CE2=2.
故选:B.
点评 本题考查的是三角形的外接圆与外心的概念和性质,掌握垂径定理、勾股定理是解题的关键.

练习册系列答案
相关题目
6.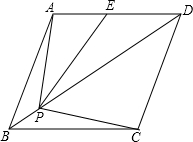 如图,菱形ABCD的边长为2,∠ABC=60°,E是AD的中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是( )
如图,菱形ABCD的边长为2,∠ABC=60°,E是AD的中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是( )
 如图,菱形ABCD的边长为2,∠ABC=60°,E是AD的中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是( )
如图,菱形ABCD的边长为2,∠ABC=60°,E是AD的中点,点P是对角线BD上的动点,当AP+PE的值最小时,PC的长是( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
13.下面各数中,最小的数是( )
| A. | 0 | B. | 0.01 | C. | -0.1 | D. | -1 |
3.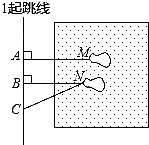 如图是某同学在体育课上跳远后留下的脚印,那么他的跳远成绩可以用图中哪条线段的长度表示( )
如图是某同学在体育课上跳远后留下的脚印,那么他的跳远成绩可以用图中哪条线段的长度表示( )
 如图是某同学在体育课上跳远后留下的脚印,那么他的跳远成绩可以用图中哪条线段的长度表示( )
如图是某同学在体育课上跳远后留下的脚印,那么他的跳远成绩可以用图中哪条线段的长度表示( )| A. | 线段AM | B. | 线段BN | C. | 线段CN | D. | 无法确定 |
7.2015年10月成立的无锡市新吴区总面积220平方公里,常住人口约55万人,下辖6个街道;2016年末,新吴区实现地区生产总值约1302亿元,用科学记数法表示该地区生产总值应记为( )
| A. | 1302×108 | B. | 1.302×103 | C. | 1.302×1010 | D. | 1.302×1011 |
8.下列计算正确的是( )
| A. | x3•x4=x12 | B. | 3x2y-5xy2=-2x2y | C. | (-x3)2÷x5=1 | D. | (-3a-2)(3a-2)=4-9a2 |
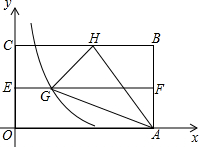 如图,在平面直角坐标系中有矩形OABC,AO=4,点E、F分别是OC和AB的中点,将矩形OABC折叠,使点B落在EF上的点G,折痕为AH,若HG延长线恰好经过点O,反比例函数y=$\frac{k}{x}$的图象过点G,求k的值.
如图,在平面直角坐标系中有矩形OABC,AO=4,点E、F分别是OC和AB的中点,将矩形OABC折叠,使点B落在EF上的点G,折痕为AH,若HG延长线恰好经过点O,反比例函数y=$\frac{k}{x}$的图象过点G,求k的值.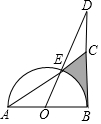 如图,已知AB是⊙O的直径,BD是⊙O的切线,线段OD与⊙O交于点E,延长AE交BD于点C,∠D=30°,AB=4.
如图,已知AB是⊙O的直径,BD是⊙O的切线,线段OD与⊙O交于点E,延长AE交BD于点C,∠D=30°,AB=4.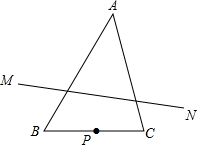 如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是2$\sqrt{6}$≤MN<4$\sqrt{2}$.
如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是2$\sqrt{6}$≤MN<4$\sqrt{2}$.