题目内容
8.计算:(1)($\frac{1}{6}$+$\frac{1}{2}$-$\frac{1}{12}$)×(-12)
(2)(1+$\frac{1}{2}$)×(-$\frac{2}{3}$)2÷$\frac{1}{3}$+(-1)3.
分析 (1)根据乘法分配律可以解答本题;
(2)根据有理数的加法、乘除法可以解答本题.
解答 解:(1)($\frac{1}{6}$+$\frac{1}{2}$-$\frac{1}{12}$)×(-12)
=$\frac{1}{6}×(-12)+\frac{1}{2}×(-12)-\frac{1}{12}×(-12)$
=(-2)+(-6)+1
=-7;
(2)(1+$\frac{1}{2}$)×(-$\frac{2}{3}$)2÷$\frac{1}{3}$+(-1)3
=$\frac{3}{2}×\frac{4}{9}×3$+(-1)
=2+(-1)
=1.
点评 本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.如图,在长方形形ABCD中,动点P从点B出发,沿BC、CD、DA运动至A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是( )


| A. | 16 | B. | 10 | C. | 18 | D. | 20 |
16.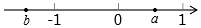 有理数a,b在数轴上对应的位置如图所示,则下列结论成立的是( )
有理数a,b在数轴上对应的位置如图所示,则下列结论成立的是( )
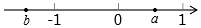 有理数a,b在数轴上对应的位置如图所示,则下列结论成立的是( )
有理数a,b在数轴上对应的位置如图所示,则下列结论成立的是( )| A. | a+b>0 | B. | a-b>0 | C. | ab>0 | D. | $\frac{a}{b}>0$ |
3.若α与β互余,且α:β=3:2,那么α的度数是( )
| A. | 18° | B. | 36° | C. | 54° | D. | 108° |
13. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )| A. | ∠A=∠D | B. | AC=BD | C. | ∠ACB=∠DBC | D. | AB=DC |

 如图:线段AD=8cm,线段AC=BD=6cm,E、F分别是线段AB、CD的中点,EF的长是6cm.
如图:线段AD=8cm,线段AC=BD=6cm,E、F分别是线段AB、CD的中点,EF的长是6cm.