题目内容
17.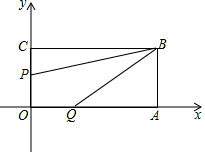 如图长方形OABC的位置如图所示,点B的坐标为(8,4),点P从点C出发向点O移动,速度为每秒1个单位;点Q同时从点O出发向点A移动,速度为每秒2个单位,设运动时间为t(0≤t≤4)
如图长方形OABC的位置如图所示,点B的坐标为(8,4),点P从点C出发向点O移动,速度为每秒1个单位;点Q同时从点O出发向点A移动,速度为每秒2个单位,设运动时间为t(0≤t≤4)(1)填空:点A的坐标为(8,0),点C的坐标为(0,4)),点P的坐标为(0,4-t).(用含t的代数式表示)
(2)当t为何值时,P、Q两点与原点距离相等?
(3)在点P、Q移动过程中,四边形OPBQ的面积是否变化?说明理由.
分析 (1)根据点坐标的定义即可解决问题;
(2)由题意OP=OQ,则有:4-t=2t,解方程即可;
(3)四边形OPBQ的面积.通过S四边形OPBQ=S矩形OABC-S△PCB-S△ABQ计算证明即可;
解答 解:(1)由题意可知点A的坐标为 (8,0),点C的坐标为 (0,4),点P的坐标为 (0,4-t).(用含t的代数式表示),
故答案分别为(8,0),(0,4),(0,4-t).
(2)依题意可知:OP=4-t,OQ=2t,若OP=OQ,则有:4-t=2t
解之得,t=$\frac{4}{3}$.
∴当t=$\frac{4}{3}$时,点P和点Q到原点的距离相等.
(3)四边形OPBQ的面积不变.理由如下:
∵S四边形OPBQ=S矩形OABC-S△PCB-S△ABQ
=32-$\frac{1}{2}$•8•t-$\frac{1}{2}$•4•(8-2t)
=32-4t-16+4t
=16.
∴四边形OPBQ的面积不变.
点评 本题考查坐标与图形的性质、矩形的性质、一元一次方程的应用,四边形的面积等知识,解题的关键是理解题意,学会用分割法求四边形面积,学会构建方程解决问题,属于中考常考题型.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
7.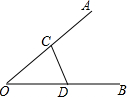 如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
 如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )
如图,在CD上找一点P,使得它到OA、OB的距离相等,则应找到( )| A. | 线段CD的中点 | B. | CD与∠AOB平分线的交点 | ||
| C. | OC垂直平分线与CD的交点 | D. | OD垂直平分线与CD的交点 |
9.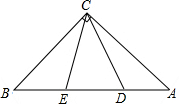 如图,在等腰直角△ABC中,AC=BC,∠BCA=90°,D、E为斜边AB上的点,∠DCE=45°,若AD=2,DE=5,则BE的长是( )
如图,在等腰直角△ABC中,AC=BC,∠BCA=90°,D、E为斜边AB上的点,∠DCE=45°,若AD=2,DE=5,则BE的长是( )
 如图,在等腰直角△ABC中,AC=BC,∠BCA=90°,D、E为斜边AB上的点,∠DCE=45°,若AD=2,DE=5,则BE的长是( )
如图,在等腰直角△ABC中,AC=BC,∠BCA=90°,D、E为斜边AB上的点,∠DCE=45°,若AD=2,DE=5,则BE的长是( )| A. | 3 | B. | $\frac{9}{2}$ | C. | $\sqrt{19}$ | D. | $\sqrt{21}$ |
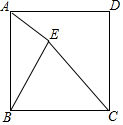 如图,点E为正方形ABCD内一点,连接AE,BE,CE,∠AEB=90°,若AE=2,BE=3,则CE=$\sqrt{10}$.
如图,点E为正方形ABCD内一点,连接AE,BE,CE,∠AEB=90°,若AE=2,BE=3,则CE=$\sqrt{10}$. 如图是“赵爽弦图”,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,根据这个图形的面积关系,可以证明勾股定理.设AD=c,AE=a,DE=b,取c=10,a-b=2.
如图是“赵爽弦图”,其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,根据这个图形的面积关系,可以证明勾股定理.设AD=c,AE=a,DE=b,取c=10,a-b=2.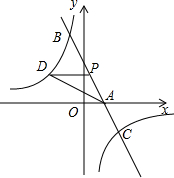 如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5),C($\frac{5}{2}$,d)两点.点P(m,n)是一次函数y1=kx+b的图象上的动点.
如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$的图象相交于B(-1,5),C($\frac{5}{2}$,d)两点.点P(m,n)是一次函数y1=kx+b的图象上的动点.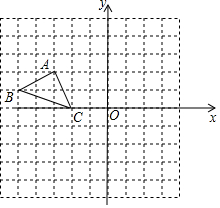 在平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,2).
在平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,2).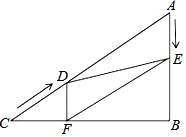 如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿
如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿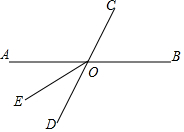 (1)已知x+y=4,x2+y2=9,求xy的值;
(1)已知x+y=4,x2+y2=9,求xy的值;