题目内容
13. 如图,AC=AE,AB=AD,BC与DE相交于F,∠1=∠2=25°.
如图,AC=AE,AB=AD,BC与DE相交于F,∠1=∠2=25°.(1)说明△ABC≌△ADE;
(2)求∠BFD的度数.
分析 (1)证出∠BAC=∠DAE,由SAS证明△ABC≌△ADE即可;
(2)由全等三角形的性质得出∠B=∠D,再由对顶角相等和三角形内角和定理得出∠BFD=∠2=25°即可.
解答 (1)证明:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
即∠BAC=∠DAE,
在△ABC和△ADE中,
$\left\{\begin{array}{l}{AC=AE}&{\;}\\{∠BAC=∠DAE}&{\;}\\{AB=AD}&{\;}\end{array}\right.$,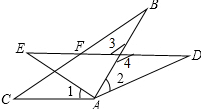
∴△ABC≌△ADE(SAS);
(2)解:如图所示:
∵△ABC≌△ADE,
∴∠B=∠D,
∵∠3=∠4,
∴∠BFD=∠2=25°.
点评 本题考查了全等三角形的判定与性质、对顶角相等的性质以及三角形内角和定理等知识;证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
2.柯桥苏宁电器超市销售每台进价分别为190元、160元的A、B两种型号的电风扇,下表是近两周的销售情况:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5100元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1720元 |
| 第二周 | 4台 | 10台 | 2960 元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5100元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?

 如图所示,已知点E是矩形ABCD边上一动点,沿A→D→C→B的路径移动,设点E经过的路径长为x,△ABE的面积是y,则下列能大致反映y与x的函数关系的图象是( )
如图所示,已知点E是矩形ABCD边上一动点,沿A→D→C→B的路径移动,设点E经过的路径长为x,△ABE的面积是y,则下列能大致反映y与x的函数关系的图象是( )



 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,A,B,D三点不在同一条直线上.
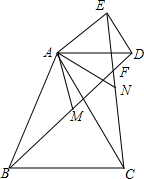
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,A,B,D三点不在同一条直线上. 如图,OC=OD,PC=PD,PM⊥OC于M,PN⊥OD于N,求证:PM=PN.
如图,OC=OD,PC=PD,PM⊥OC于M,PN⊥OD于N,求证:PM=PN.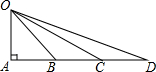 如图,在Rt△OAD中,∠A=90°,B,C在AD边上,且OA=AB=BC=CD,有下列结论:①△AOB∽△BOD:②△BOC∽△BDO:③△COD∽△BDO,其中成立的有②(选填序号)
如图,在Rt△OAD中,∠A=90°,B,C在AD边上,且OA=AB=BC=CD,有下列结论:①△AOB∽△BOD:②△BOC∽△BDO:③△COD∽△BDO,其中成立的有②(选填序号)