Question

18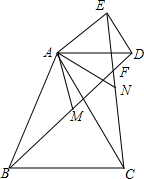．如图，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，A，B，D三点不在同一条直线上．
（1）试判断BD与CE之间的数量关系；
（2）设BD与CE交点为F，若∠BAC=45°，求∠BFC的度数；
（3）分别取BD与CE中点M，N，连接AM，AN，试判断AM与AN之间的关系．

Answer 1

分析 （1）根据已知条件得到∠BAD=∠CAE，证得△ABD≌△CAE，根据全等三角形的性质即可得到结论；
（2）根据全等三角形的性质得到∠ABD=∠ACE，推出A，B，C，F四点共圆，根据圆周角定理即可得到结论；
（3）根据线段的中点的定义得到BM=CN，推出△ABM≌△ACN，根据全等三角形的性质即可得到即可结论．

解答 解：（1）BD=CE，
∵∠BAC=∠DAE，
∴∠BAC+∠CAD=∠DAE+∠CAD，
即∠BAD=∠CAE，
在△ABD与△CAE中，
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$，
∴△ABD≌△CAE，
∴BD=CE；

（2）∵△ABD≌△CAE，
∴∠ABD=∠ACE，
∴A，B，C，F四点共圆，
∴∠BFC=∠BAC=45°；

（3）AM=AN，
∵BD=CE，
∵M，N是BD与CE中点，
∴BM=CN，
在△ABM与△ACN中，
$\left\{\begin{array}{l}{AB=AC}\\{∠ABM=∠ACN}\\{BM=CN}\end{array}\right.$，
∴△ABM≌△ACN，
∴AM=AN．

点评 本题考查了全等三角形的判定和性质，四点共圆，圆周角定理，熟练掌握全等三角形的判定和性质是解题的关键．