题目内容
7.象棋比赛中.每名选手与其他选手比赛一场,每局胜者得2分,负者得0分,平局每人记1分.今有2位同学统计全部选手得分的总和分别是80,90,经核实,只有一位同学是正确的,求比赛共有多少名选手?分析 每局的得分均为2分,2人的比赛只有一局;局数=$\frac{1}{2}$×选手数×(选手数-1);等量关系为:2×局数=所得分数,把分数代入看哪个有整数解即可.
解答 解:设这次比赛中共有x名选手参加,
2×$\frac{1}{2}$×x(x-1)=80,
解得x不为整数,故错误;
2×$\frac{1}{2}$×x(x-1)=90,
解得x1=10,x2=-9(不合题意,舍去)
∵只有一位同学是正确的,
∴正确的分数90,共有10名选手参加比赛.
点评 本题考查了一元二次方程的应用;得到局数是解决本题的难点;判断出相应的分数是解决本题的易错点.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
18.下列计算正确的是( )
| A. | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{15}=3\sqrt{5}$ | D. | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ |
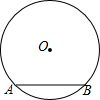 如图,在⊙O中,弦AB的长为8,圆心O到AB的距离为3,则⊙O的半径是5;
如图,在⊙O中,弦AB的长为8,圆心O到AB的距离为3,则⊙O的半径是5;