题目内容
12.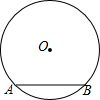 如图,在⊙O中,弦AB的长为8,圆心O到AB的距离为3,则⊙O的半径是5;
如图,在⊙O中,弦AB的长为8,圆心O到AB的距离为3,则⊙O的半径是5;变化①:⊙O中有一点C,过这点最长的弦为10,最短的弦为6,则点O与C的距离是4;
变化②:在上题的条件下,过C点的弦中长度为整数的弦有8条.
分析 (1)根据垂径定理和勾股定理求解;
(2)根据题意,得最长的弦即直径是10,最短的弦即过点C垂直于OC的弦AB,连接OA,根据勾股定理以及垂径定理即可求得;
(3)求出过P点的弦的长度的取值范围,取特殊解,根据对称性综合求解.
解答 解:(1)如图1,过点O作OE⊥AB,
在直角△AOE中,AE=4,OE=3,
根据勾股定理得到OA=5,
则⊙O的半径是5,
故答案为:5;
(2)如图2,连接OA,根据题意,OA=10÷2=5,AC=6÷2=3,
∴OC=$\sqrt{{OA}^{2}{-AC}^{2}}$=$\sqrt{{5}^{2}{-3}^{2}}$=4,
故答案为:4;
(3)∵过C点最长的弦为10,最短的弦为6,
∴过点C的弦的弦长可以是7,8,9各两条,总共有8条长度为整数的弦.
故答案是:8.
点评 本题主要考查了垂径定理和勾股定理,注意理解最短和最长的弦是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.如果一元一次方程3x-b=0的根x=2,那么一次函数y=3x-b的图象一定过点( )
| A. | (0,2) | B. | (2,0) | C. | (-2,0) | D. | (0,-2) |
4.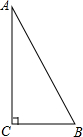 如图,Rt△ABC,∠C=90°,AB=13,BC=5,则cosB的值为( )
如图,Rt△ABC,∠C=90°,AB=13,BC=5,则cosB的值为( )
 如图,Rt△ABC,∠C=90°,AB=13,BC=5,则cosB的值为( )
如图,Rt△ABC,∠C=90°,AB=13,BC=5,则cosB的值为( )| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{5}{12}$ | D. | $\frac{13}{3}$ |