题目内容
1.如图(1),在平面直角坐标系中,直线$y=\sqrt{3}x+6$与两坐标轴分别交于A、B两点,M为y轴正半轴上一点,⊙M过A、B两点,交x轴正半轴于点C,过B作x轴的平行线l,N点的坐标为(-12,5),⊙N与直线l相切于点D.(1)求∠ABO的度数及圆心M的坐标;
(2)若⊙N以每秒1个单位的速度沿直线l向右平移,同时直线AB沿x轴负方向匀速平移,当⊙N第一次与⊙M相切时,直线AB也恰好与⊙N第一次相切,求直线AB每秒平移多少个单位长度?
(3)如图(2),P为直线l上的一个动点,过P作AB的垂线分别交线段BC、x轴于Q、R两点,过P作x轴的垂线,垂足为S(S在A点的左侧).当P点运动时,BQ-AS的值是否改变?若不变,请求其值;若改变,请求其值变化的范围.

分析 (1)由直线AB解析式可知A,B两点的坐标,在Rt△AOB中利用三角函数可求得∠ABO,设⊙M交y轴负半轴于点N,进一步可求得BN的长度,可求得M的坐标;
(2)由条件可求得⊙N的圆心移动的距离,可求得其移动的时间,进一步求出直线AB移动的距离,则可求得其平移的速度;
(3)由条件可证明CR=CQ,且∠PRS=30°,可求得PS及PR,SR的长度,且可证明△ABC为等边三角形,所以得出SA-BQ为定值.
解答 解:(1)直线$y=\sqrt{3}x+6$中令x=0,可得y=6,令y=0可得x=-2$\sqrt{3}$,
∴OA=2$\sqrt{3}$,OB=6,
∴tan∠ABO=$\frac{AO}{BO}$=$\frac{\sqrt{3}}{3}$,
∴∠ABO=30°,
如图1,连接MA,则MA=MB,且OM=OB-MB=6-MA,
在Rt△AOM中,由勾股定理可得AM2=AO2+(6-MA)2,
解得MA=4,则OM=2,所以M坐标为(0,2);
(2)N点坐标为(-12,5),且D到x轴的距离等于OB,故⊙N的半径为1,
当⊙N与⊙M第一次相切时,即在y轴左边与⊙M相外切,
如图2,连接MN,过N作NE⊥x轴,过M作NE⊥NE,交于点E,
则由两圆相外切可知MN=4+1=5,NE=5-2=3,由勾股定理可求得ME=4,即此时N点的坐标为(-4,5),
所以⊙N的移动距离为-4-(-12)=8,其移动速度为每秒1个单位长度,所以⊙N移动的时间为8秒,
设直线AB移动后与x轴、y轴相交于点A′、B′,由题意可知直线A′B′为两圆的公切线,设切点为F,则FM=4,
在Rt△MFB′中,∠A′B′O=∠ABO=30°,所以MB′=2MF=8,所以OB′=2+8=10,
所以直线A′B′的解析式为y=$\sqrt{3}$x+10,令y=0可得x=-$\frac{10\sqrt{3}}{3}$,所以OA′=$\frac{10\sqrt{3}}{3}$,
由(1)知OA=2$\sqrt{3}$,所以AA′=OA′-OA=$\frac{4\sqrt{3}}{3}$,
其移动时间为8秒,所以其速度为$\frac{4\sqrt{3}}{3}$÷8=$\frac{\sqrt{3}}{6}$,
即求直线AB每秒平移了$\frac{\sqrt{3}}{6}$个单位长度;
(3)在图1中,BO⊥AC,且BO过圆心M,
∴AO=OC=2$\sqrt{3}$=AB,且∠BAO=60°,
∴△ABC为等边三角形,
∴∠ABC=60°,AC=BC,
∵PR⊥AB,
∴∠BQC=∠CQR=30°,∠ARP=30°,
∴CR=CQ,
∴BQ=BC-CQ=AC-CR=4$\sqrt{3}$-CR,
∵PS⊥SR,
∴PS=OB=6,
∴PR=2PS=12,
在Rt△PSR中可求得SR=6$\sqrt{3}$,
∴SA=SR-AC-CR=6$\sqrt{3}$-4$\sqrt{3}$-CR=2$\sqrt{3}$-CR,
∴BQ-SA=4$\sqrt{3}$-CR-(2$\sqrt{3}$-CR)=2$\sqrt{3}$,
∴BQ-AS的值不改变,其值为2$\sqrt{3}$.
点评 本题主要考查切线的性质及等边三角形的判定和性质、直角三角形的性质的综合应用,在第(2)问中确定出直线AB移动的距离是解题的关键,在第(3)问中证明CQ=CR是解题的关键.

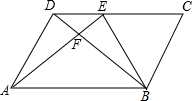 如图,在平行四边形ABCD中,DE:CE=2:3,则S△DEF:S△EFB:S△FAB等于( )
如图,在平行四边形ABCD中,DE:CE=2:3,则S△DEF:S△EFB:S△FAB等于( )| A. | 4:10:25 | B. | 4:9:25 | C. | 2:3:25 | D. | 2:5:25 |
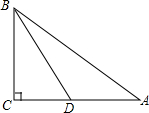 如图,△ABC为直角三角形,∠C=90°,AC=4,CB=3,AB=5,BD为△ABC的中线,AE平分∠BAC交BD于E,则E到BC的距离为$\frac{10}{7}$.
如图,△ABC为直角三角形,∠C=90°,AC=4,CB=3,AB=5,BD为△ABC的中线,AE平分∠BAC交BD于E,则E到BC的距离为$\frac{10}{7}$.