题目内容
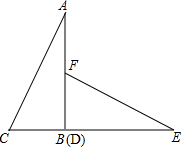 两张全等的直角三角形纸片如图摆放,期中B、D重合,B、C、E在同一条直线上,已知AB=4,BC=3,现将△DEF沿射线BC方向平行移动,在整个运动过程中,要使△ACE成为等腰三角形,求△DEF平移的距离.
两张全等的直角三角形纸片如图摆放,期中B、D重合,B、C、E在同一条直线上,已知AB=4,BC=3,现将△DEF沿射线BC方向平行移动,在整个运动过程中,要使△ACE成为等腰三角形,求△DEF平移的距离.考点:平移的性质,等腰三角形的判定
专题:
分析:利用勾股定理列式求出AC,分①AC=AE时,利用等腰三角形三线合一的性质可得BE=BC,然后求出平移的距离;②AC=CE时,分点E在点C的右边与左边两种情况求解;③AE=CE时,再利用∠C的正切值求出CE,然后求出平移的距离即可.
解答:解:在Rt△ABC中,AC=
=
=5,
①AC=AE时,BE=BC=3,
∵AB=4,BC=3,
∴平移距离=3+4-3×2=1;
②AC=CE时,若点E在点C的右边,则平移距离=3+4-5=2,
若点E在点C的左边,则平移距离=3+4+5=12;
③AE=CE时,CE=
ACtan∠C=
×5×
=
,
平移距离=3+4-
=
,
综上所述,要使△ACE成为等腰三角形,△DEF平移的距离为1、2、12或
.
| AB2+BC2 |
| 42+32 |
①AC=AE时,BE=BC=3,
∵AB=4,BC=3,
∴平移距离=3+4-3×2=1;
②AC=CE时,若点E在点C的右边,则平移距离=3+4-5=2,
若点E在点C的左边,则平移距离=3+4+5=12;
③AE=CE时,CE=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 10 |
| 3 |
平移距离=3+4-
| 10 |
| 3 |
| 11 |
| 3 |
综上所述,要使△ACE成为等腰三角形,△DEF平移的距离为1、2、12或
| 11 |
| 3 |
点评:本题考查了平移的性质,等腰三角形的判定,勾股定理,难点在于分情况讨论.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
a是实数,a2+1与2a的大小关系是( )
| A、a2+1≥2a |
| B、a2+1>2a |
| C、a2+1与2a的大小关系随a的变化而改变 |
| D、当a>0时,a2+1≤a;当a<0时,a2+1≥2a |