题目内容
 如图,三角形ABO的面积为12,且AO=AB,双曲线y=
如图,三角形ABO的面积为12,且AO=AB,双曲线y=| k |
| x |
考点:全等三角形的判定与性质,反比例函数系数k的几何意义,等腰三角形的性质
专题:
分析:根据等腰三角形的性质,可得OC=BC,根据三角形中位线的性质,可得CE=BE,DE=
AC,根据三角形的面积,等量代换,可得答案.
| 1 |
| 2 |
解答:解:作AC⊥OB与点C,作DE⊥OB于点E, ,
,
∵OA=AB,
∴OC=BC.
∵点D为AB的中点,
∴DE是△ABC的中位线,
∴CE=BE,DE=
AC,
OE=
OB.
∵S△AOB=
AC•OB=12,
DE•
OE=12,
DE•OE=9,
设点D的坐标为(x,y),点D在反比例函数y=
的图象上,
∴k=xy=OE•DC=9,
故答案为:9.
 ,
,∵OA=AB,
∴OC=BC.
∵点D为AB的中点,
∴DE是△ABC的中位线,
∴CE=BE,DE=
| 1 |
| 2 |
OE=
| 3 |
| 4 |
∵S△AOB=
| 1 |
| 2 |
DE•
| 4 |
| 3 |
DE•OE=9,
设点D的坐标为(x,y),点D在反比例函数y=
| k |
| x |
∴k=xy=OE•DC=9,
故答案为:9.
点评:本题考查了反比例函数k的几何意义,利用了等腰三角形的性质,三角形的中位线,反比例函数k的几何意义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
a是实数,a2+1与2a的大小关系是( )
| A、a2+1≥2a |
| B、a2+1>2a |
| C、a2+1与2a的大小关系随a的变化而改变 |
| D、当a>0时,a2+1≤a;当a<0时,a2+1≥2a |
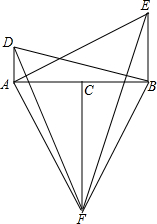 如图,点C在线段AB上,DA⊥AB,BE⊥AB,FC⊥AB,且DA=BC,AC=BE,FC=AB.
如图,点C在线段AB上,DA⊥AB,BE⊥AB,FC⊥AB,且DA=BC,AC=BE,FC=AB. 如图,AC平分∠BAD,∠BAC=∠C,AB∥DE.求证:
如图,AC平分∠BAD,∠BAC=∠C,AB∥DE.求证: