��Ŀ����
4����ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬������OACB�Ķ���A��B�ֱ���x����y���ϣ���֪A������Ϊ��a��0����B������Ϊ��0��b������a��b����$\sqrt{a+b-16}$+|2a-b-2|=0��DΪy����һ�㣬������Ϊ��0��2������P�ӵ�A������ÿ��1����λ���ٶ����߶�AC-CB�ķ����˶�������P���B�غ�ʱֹͣ�˶����˶�ʱ��Ϊt�룮��1������P������Cʱ����ֱ��DP�ĺ�������ʽ��
��2�������OPD�����S����t�ĺ�������ʽ��
����ͼ�ڣ��ѳ���������OP�۵�����B�Ķ�Ӧ��B��ǡ������AC���ϣ����P�����꣮
��3����P���˶��������Ƿ����ʹ��BDPΪ���������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
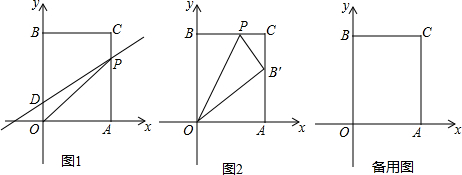
���� ��1�����A��B������꣬�Ӷ����C�����꣬��ֱ��DP����ʽΪy=kx+b����D��C����������k��b��ֵ������ȷ��������ʽ��
��2���ٵ�P��AC��ʱ��������ODP��OD���Ϊ�̶�ֵ�������ʱ�������P��BC��ʱ���ױ�ODΪ�̶�ֵ����ʾ���ߣ������г�S��t�Ĺ�ϵʽ��
�ڵ���B�Ķ�Ӧ��B��ǡ������AC����ʱ���ؼ����ɶ������������ʱP���ꣻ
��3�����ڣ��ֱ���BD��DP��BPΪ�ױ�����������ǣ����ù��ɶ�����ͼ���������������P���꼴�ɣ�
���  �⣺��1����a��b����$\sqrt{a+b-16}$+|2a-b-2|=0��
�⣺��1����a��b����$\sqrt{a+b-16}$+|2a-b-2|=0��
��$\left\{\begin{array}{l}{a+b-16=0}\\{2a-b-2=0}\end{array}\right.$�����$\left\{\begin{array}{l}{a=6}\\{b=10}\end{array}\right.$��
���������6��0����B��������0��10����
��C��6��10����
���ʱֱ��DP����ʽΪy=kx+b����ͼ1��
��D��0��2����C��6��10������ã�$\left\{\begin{array}{l}{b=2}\\{6k+b=10}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=2}\end{array}\right.$��
���ʱֱ��DP����ʽΪy=$\frac{4}{3}$x+2��
��2���ٵ���P���߶�AC��ʱ��OD=2����Ϊ6��S=6��
����P���߶�BC��ʱ��OD=2����Ϊ6+10-t=16-t��S=$\frac{1}{2}$��2����16-t��=-t+16��
����P��m��10������PB=PB��=m����ͼ2��
��OB��=OB=10��OA=6��
��AB��=$\sqrt{O{B��}^{2}-O{A}^{2}}$=8��
��B��C=10-8=2��
��PC=6-m��
��m2=22+��6-m��2�����m=$\frac{10}{3}$
���ʱ��P�������ǣ�$\frac{10}{3}$��10����
��3�����ڣ�����Ϊ��
����BDPΪ���������Σ�������������ǣ���ͼ3��
�ٵ�BD=BP1=OB-OD=10-2=8��
��Rt��BCP1��BP1=8��BC=6��
���ݹ��ɶ����ã�CP1=$\sqrt{{8}^{2}-{6}^{2}}$=2$\sqrt{7}$��
��AP1=10-2$\sqrt{7}$����P1��6��10-2$\sqrt{7}$����
�ڵ�BP2=DP2ʱ����ʱP2��6��6����
�۵�DB=DP3=8ʱ��
��Rt��DEP3��DE=6��
���ݹ��ɶ����ã�P3E=$\sqrt{{8}^{2}-{6}^{2}}$=2$\sqrt{7}$��
��AP3=AE+EP3=2$\sqrt{7}$+2����P3��6��2$\sqrt{7}$+2����
���ϣ����������P����Ϊ��6��6����6��2$\sqrt{7}$+2����6��10-2$\sqrt{7}$����
���� ��������һ�κ����ۺ��⣬�漰��֪ʶ�У�����ϵ����ȷ��һ�κ�������ʽ��������ͼ�����ʣ����������ε����ʣ����ɶ����������˷������۵�˼�룬�������մ���ϵ�����ǽⱾ���һ�ʵĹؼ���

 ��ͼ��ʾ��Բ��ͼ��������ͬ�뾶��Բ��Բ�����ɵģ�����Բ��Ͷ�����ڣ���������ں�ɫ����ĸ���Ϊ��������
��ͼ��ʾ��Բ��ͼ��������ͬ�뾶��Բ��Բ�����ɵģ�����Բ��Ͷ�����ڣ���������ں�ɫ����ĸ���Ϊ��������| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{5}$ |
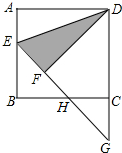 ��ͼ����E��������ABCD�ı�AB��һ�㣬�ҡ�ADE=22.5�㣬����ADE��DE���۵õ���FDE���ӳ�EF��BC�ڵ�H����DC���ӳ����ڵ�G����ͼ�����еĵ����������ǡ�EBH����GHC����EDG������������������������ȫ���оٳ�������
��ͼ����E��������ABCD�ı�AB��һ�㣬�ҡ�ADE=22.5�㣬����ADE��DE���۵õ���FDE���ӳ�EF��BC�ڵ�H����DC���ӳ����ڵ�G����ͼ�����еĵ����������ǡ�EBH����GHC����EDG������������������������ȫ���оٳ�������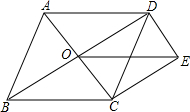 ��ͼ����O������ABCD�Խ��ߵĽ��㣬DE��AC��CE��BD������OE��
��ͼ����O������ABCD�Խ��ߵĽ��㣬DE��AC��CE��BD������OE��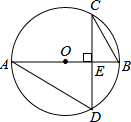 ��ͼ���ڡ�O�У�CD��AB��E������BAD=30�㣬��BE=2����CD=4$\sqrt{3}$��
��ͼ���ڡ�O�У�CD��AB��E������BAD=30�㣬��BE=2����CD=4$\sqrt{3}$��