题目内容
16.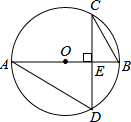 如图,在⊙O中,CD⊥AB于E,若∠BAD=30°,且BE=2,则CD=4$\sqrt{3}$.
如图,在⊙O中,CD⊥AB于E,若∠BAD=30°,且BE=2,则CD=4$\sqrt{3}$.
分析 先根据圆周角定理求出∠C的度数,再由CD⊥AB可知∠CEB=90°,CD=2CE,由直角三角形的性质求出BC的长,根据勾股定理求出CE的长,进而可得出结论.
解答 解:∵∠BAD=30°,BE=2,
∴∠C=∠BAD=30°.
∵CD⊥AB,
∴∠CEB=90°,CD=2CE,
∴BC=2BE=4,
∴CE=$\sqrt{{BC}^{2}-{BE}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴CD=2CE=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.对于反比例函数y=$\frac{2}{x}$,下列说法正确的是( )
| A. | 图象经过点(-2,1) | B. | 图象位于第二、第四象限 | ||
| C. | y随x的增大而减小 | D. | 当x>1时,0<y<2 |
 如图.点E是菱形ABCD边AD反向延长线上的一点,连结CE交AB于F,连结BE,过点F作FH∥AE交BE于H,求证:AF=HF.
如图.点E是菱形ABCD边AD反向延长线上的一点,连结CE交AB于F,连结BE,过点F作FH∥AE交BE于H,求证:AF=HF.