题目内容
13.分解因式(1)a3-9a
(2)3x2-6xy+x
(3)n2(m-2)+n(2-m)
(4)-4x2+4xy+y2
(5)a2+2a-8.
分析 (1)首先提取公因式a,进而利用平方差公式分解因式得出即可;
(2)直接提取公因式x,分解因式得出即可;
(3)直接提取公因式n(m-2),分解因式得出即可;
(4)利用配方法,即可解答;
(5)原式利用十字相乘法分解即可.
解答 解:(1)原式=a(a2-9)
=a(a+3)(a-3);
(2)原式=x(3x-6y+1);
(3)原式=n(m-2)(n-1);
(4)-4x2+4xy+y2
=4x2+4xy+y2-8x2
=$(2x+y)^{2}-(2\sqrt{2}x)^{2}$
=(2x+y+2$\sqrt{2}$x)(2x$+y-2\sqrt{2}x$)
=$[(2+2\sqrt{2})x+y][(2-2\sqrt{2})x+y]$.
(5)原式=(a-2)(a+4).
点评 本题考查了因式分解,解决本题的关键是选择合适的方法进行因式分解.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
18.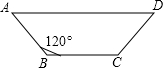 如图,某村计划修一条水渠,横截面是等腰梯形,底角为120°,两腰与底BC的和为4m,则梯形的最大面积为( )
如图,某村计划修一条水渠,横截面是等腰梯形,底角为120°,两腰与底BC的和为4m,则梯形的最大面积为( )
 如图,某村计划修一条水渠,横截面是等腰梯形,底角为120°,两腰与底BC的和为4m,则梯形的最大面积为( )
如图,某村计划修一条水渠,横截面是等腰梯形,底角为120°,两腰与底BC的和为4m,则梯形的最大面积为( )| A. | $4\sqrt{3}{m^2}$ | B. | 9m2 | C. | 3m2 | D. | $\frac{{4\sqrt{3}}}{3}{m^2}$ |
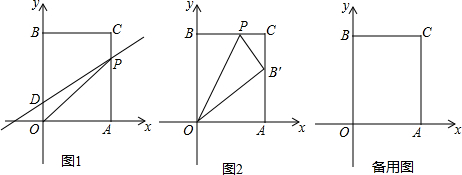
 如图.点E是菱形ABCD边AD反向延长线上的一点,连结CE交AB于F,连结BE,过点F作FH∥AE交BE于H,求证:AF=HF.
如图.点E是菱形ABCD边AD反向延长线上的一点,连结CE交AB于F,连结BE,过点F作FH∥AE交BE于H,求证:AF=HF. 如图,正方形ABCD的边长为1,以直线AB为轴将正方形旋转一周,所得一个圆柱,求:
如图,正方形ABCD的边长为1,以直线AB为轴将正方形旋转一周,所得一个圆柱,求: