题目内容
14.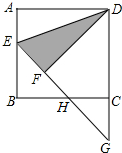 如图,点E是正方形ABCD的边AB上一点,且∠ADE=22.5°,将△ADE沿DE翻折得到△FDE,延长EF交BC于点H,交DC的延长线于点G,则图中所有的等腰三角形是△EBH、△GHC、△EDG(将符合条件的所有三角形全部列举出来).
如图,点E是正方形ABCD的边AB上一点,且∠ADE=22.5°,将△ADE沿DE翻折得到△FDE,延长EF交BC于点H,交DC的延长线于点G,则图中所有的等腰三角形是△EBH、△GHC、△EDG(将符合条件的所有三角形全部列举出来).
分析 在Rt△AED中,可求得∠AED=67.5°然后再求得∠BEH=45°,从而可判断△EBH和△HCG的形状,然后再证明∠DEG=∠EDG,可判断△EDG的形状.
解答 解:∵∠AED+ADE=90°,∠ADE+∠EDG=90°,
∴∠AED=∠EDG.
由翻折的性质可知:∠AED=∠GED.
∴∠DEG=∠EDG.
∴EG=DG.
∴△EDG为等腰三角形.
∵∠ADE=22.5°,
∴∠AED=∠DEG=67.5°.
∴∠BEH=180°-∠AED-∠DEG=45°.
∴∠BHE=∠CHG=∠HGC=45°.
∴∠BEH=∠EHB,∠CHG=∠CGH.
∴BE=BH,CH=CG.
∴△EBH、△GHC为等腰三角形.
故答案为:△EBH、△GHC、△EDG.
点评 本题主要考查的是翻折的性质、等腰三角形的判定、三角形内角和定理的应用,掌握等腰三角形的判定定理是解题的关键.

练习册系列答案
相关题目
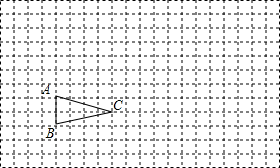 作图题:如图所示,△ABC在方格纸中
作图题:如图所示,△ABC在方格纸中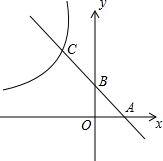 如图,直线y=-2x+1分别交x轴,y轴于点A,B,交反比例函数y=$\frac{k}{x}$的图象于点C,CB:BA=2:1.
如图,直线y=-2x+1分别交x轴,y轴于点A,B,交反比例函数y=$\frac{k}{x}$的图象于点C,CB:BA=2:1.