题目内容
17.某商场销售A、B两种型号计算器,A型号计算器的进货价格为每台30元,B型号计算器的进货价格为每台40元.商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.(1)分别求商场销售A、B两种型号计算器每台的销售价格.
(2)商场准备用不多于2 500元的资金购进A、B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?【利润=销售价格-进货价格】
分析 (1)首先设A种型号计算器的销售价格是x元,B种型号计算器的销售价格是y元,根据题意可等量关系:①5台A型号和1台B型号计算器,可获利润76元;②销售6台A型号和3台B型号计算器,可获利润120元,根据等量关系列出方程组,再解即可;
(2)根据题意表示出所用成本,进而得出不等式求出即可.
解答 (1)设A种型号计算器的销售价格是x元,B种型号计算器的销售价格是y元.
根据题意,得$\left\{\begin{array}{l}5(x-30)+(y-40)=76\\ 6(x-30)+3(y-40)=120.\end{array}\right.$
解得$\left\{\begin{array}{l}x=42\\ y=56.\end{array}\right.$(
答:商场销售A、B两种型号计算器的销售价格分别为42元、56元.
(2)设需要购进A型号的计算器a台.
根据题意,得30a+40(70-a)≤2500.
解得a≥30.
答:最少需要购进A型号的计算器30台.
点评 此题主要考查了一元一次不等式的应用以及二元一次方程组的应用,根据题意得出总的进货费用是解题关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图,在矩形ABCD中,点E、F分别在AB、CD上,且CF=AE.
如图,在矩形ABCD中,点E、F分别在AB、CD上,且CF=AE. 尺规作图:
尺规作图: 如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC,求证:△ABD≌△EDC.
如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC,求证:△ABD≌△EDC.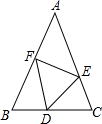 如图,在△ABC中,AB=AC,点D、E、F分别在△ABC的三条边上,且BF=CD,BD=CE.
如图,在△ABC中,AB=AC,点D、E、F分别在△ABC的三条边上,且BF=CD,BD=CE.