Question

6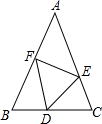．如图，在△ABC中，AB=AC，点D、E、F分别在△ABC的三条边上，且BF=CD，BD=CE．
（1）求证：△DFE是等腰三角形；
（2）若∠A=56°，求∠EDF的度数．

Answer 1

分析 （1）由SAS可得△FBD≌△DCE，得出DF=ED，第一问可求解；
（2）由角之间的转化，从而可求解∠EDF的大小．

解答 证明：（1）：∵AB=AC∴∠B=∠C，
在△FBD与△DCE中$\left\{\begin{array}{l}{BF=CD}\\{∠B=∠C}\\{BD=CE}\end{array}\right.$
∴△FBD≌△DCE．
∴DF=ED，即△DEF是等腰三角形
（2）∵AB=AC，∠A=56°，∴∠B=∠C=$\frac{1}{2}（180°-56°）=62°$．
∴∠EDF=∠B=62°．

点评 本题主要考查了全等三角形的判定及性质以及等腰三角形的判定和性质问题，能够熟练掌握三角形的性质求解一些简单的计算、证明等问题．