题目内容
13.一个三角形的两边长为3和5,第三边长为方程x2-5x+6=0的根,则这个三角形的周长为11.分析 直接利用因式分解法解方程,进而利用三角形三边关系得出答案.
解答 解:x2-5x+6=0
(x-3)(x-2)=0,
解得:x1=3,x2=2,
∵一个三角形的两边长为3和5,
∴第三边长的取值范围是:2<x<8,
则第三边长为:3,
∴这个三角形的周长为:11.
故答案为:11.
点评 此题主要考查了因式分解法解方程以及三角形三边关系,正确掌握三角形三边关系是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2. 如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=20°,则∠EPF=( )
如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=20°,则∠EPF=( )
 如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=20°,则∠EPF=( )
如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=20°,则∠EPF=( )| A. | 70° | B. | 65° | C. | 55° | D. | 45° |
3.已知$\left\{{\begin{array}{l}x=1\\ y=1\end{array}}\right.$,$\left\{{\begin{array}{l}x=2\\ y=3\end{array}}\right.$是关于x,y的二元一次方程y=kx+b的解,则k,b的值是( )
| A. | k=1,b=0 | B. | k=-1,b=2 | C. | k=2,b=-1 | D. | k=-2,b=1 |
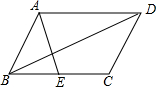 如图,在平行四边形ABCD中,AD=10,BD=12,点E为BC边上任意一点,连接AE、DE,当AE=5,BE=3时,平行四边形ABCD的面积是$\frac{600}{13}$.
如图,在平行四边形ABCD中,AD=10,BD=12,点E为BC边上任意一点,连接AE、DE,当AE=5,BE=3时,平行四边形ABCD的面积是$\frac{600}{13}$.