Question

3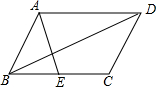．如图，在平行四边形ABCD中，AD=10，BD=12，点E为BC边上任意一点，连接AE、DE，当AE=5，BE=3时，平行四边形ABCD的面积是$\frac{600}{13}$．

Answer 1

分析 过点A作AM⊥BC于点M，过点D作DN⊥BC的延长线于点N，设BM=a，AM=b，则ME=3-a，DN=AM=b，BN=10+a．在Rt△AME和Rt△BND中，由勾股定理即可得出关于a、b的二元二次方程组，解方程组即可得出b值，再根据平行四边形的面积公式即可得出结论．

解答 解：过点A作AM⊥BC于点M，过点D作DN⊥BC的延长线于点N，如图所示．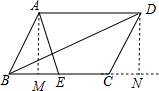
设BM=a，AM=b，则ME=3-a，DN=AM=b，BN=10+a．
在Rt△AME中，AM²=AE²-ME²=5²-（3-a）²=b²①；
在Rt△BND中，DN²=BD²-BN²=12²-（10+a）²=b²②．
联立①②得：$\left\{\begin{array}{l}{25-（3-a）^{2}={b}^{2}}\\{144-（10+a）^{2}={b}^{2}}\end{array}\right.$，解得：$\left\{\begin{array}{l}{a=\frac{14}{13}}\\{b=\frac{60}{13}}\end{array}\right.$或$\left\{\begin{array}{l}{a=\frac{14}{13}}\\{b=-\frac{60}{13}}\end{array}\right.$（舍去）．
S_{平行四边形ABCD}=AD•AM=10×$\frac{60}{13}$=$\frac{600}{13}$．
故答案为：$\frac{600}{13}$．

点评 本题考查了平行四边形的性质、勾股定理以及解二元二次方程组，解题的关键是求出边BC上的高AM的长度．本题属于中档题，难度不大，解决该题型题目时，借助于勾股定理得出方程组是关键．