题目内容
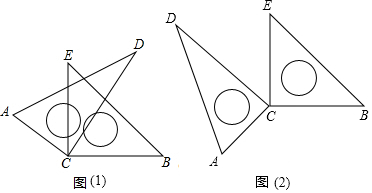
18.数学活动课上,小聪同学摆弄着自己刚购买的一套三角板,将两块直角三角板的直角顶点C叠放在一起,然后转动三角板,在转动过程中,请解决以下问题:(1)如图(1):当∠DCE=30°时,∠ACB+∠DCE=30°,若∠DCE为任意锐角时,你还能求出∠ACB与∠DCE的数量关系吗?若能,请求出;若不能,请说明理由.
(2)当转动到图(2)情况时,∠ACB与∠DCE有怎样的数量关系?请说明理由.
分析 (1)当∠DCE=30°时,利用互余计算出∠BCD,然后可得到∠ACB+∠DCE的度数;若∠DCE为任意锐角时,利用∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,然后计算出∠ACB+∠DCE=180°;
(2)利用周角定义得到∠ACD+∠ECB+∠ACB+∠DCE=360°所以∠ECD+∠ACB=360°-(∠ACD+∠ECB)=180°.
解答 解:(1)∠ACB+∠DCE=180°;
若∠DCE为任意锐角时,∠ACB+∠DCE=180°,
理由如下:∵∠ACE+∠DCE=90°,
∠BCD+∠DCE=90°,
∴∠ACB+∠DCE=∠ACE+∠DCE+∠BCD+∠DCE=90°+90°=180°;
(2)∠ACB+∠DCE=180°.
理由如下:∵∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,
∴∠ECD+∠ACB=360°-(∠ACD+∠ECB)=360°-180°=180°.
故答案为30°.
点评 本题考查了余角和补角:等角的补角相等.等角的余角相等;余角和补角计算的应用,常常与等式的性质、等量代换相关联.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列命题中,真命题是( )
| A. | 两条对角线互相垂直平分的四边形是矩形 | |
| B. | 有一条对角线平分一组对角的四边形是菱形 | |
| C. | 两条对角线相等的四边形是矩形 | |
| D. | 一组对边平行,一组对角相等的四边形是平行四边形 |
6.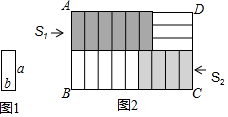 已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,AB=3b+a,当BC的长度变化时,左上角阴影面积S1与左下角阴影面积S2的差没有变化,在a,b之间的关系应满足( )
已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,AB=3b+a,当BC的长度变化时,左上角阴影面积S1与左下角阴影面积S2的差没有变化,在a,b之间的关系应满足( )
 已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,AB=3b+a,当BC的长度变化时,左上角阴影面积S1与左下角阴影面积S2的差没有变化,在a,b之间的关系应满足( )
已知8个长为a,宽为b的小长方形(如图1),不重叠无空隙地摆放(如图2),在长方形ABCD中,AB=3b+a,当BC的长度变化时,左上角阴影面积S1与左下角阴影面积S2的差没有变化,在a,b之间的关系应满足( )| A. | 5b=2a | B. | 2b=a | C. | 3b=a | D. | 5b=3a |
13.以下列各组线段为边,能组成三角形的是( )
| A. | 3cm,5cm,8cm | B. | 8cm,7cm,13cm | C. | 13cm,12cm,31cm | D. | 7cm,7cm,15cm |
3.为了了解2015年我市七年级学生期末考试的数学成绩,从中随机抽取了1000名学生的数学成绩进行分析,下列说法正确的是( )
| A. | 2015年我市七年级学生是总体 | |
| B. | 样本容量是1000 | |
| C. | 1000名七年级学生是总体的一个样本 | |
| D. | 每一名七年级学生是个体 |

 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )
如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )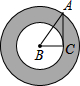 如图,在Rt△ABC中,∠C=90°,将其绕B点顺时针旋转一周,则分别以BA,BC为半径的圆形形成一圆环(阴影部分),为求该圆环的面积,只需测量一条线段的长度,这条线段就是( )
如图,在Rt△ABC中,∠C=90°,将其绕B点顺时针旋转一周,则分别以BA,BC为半径的圆形形成一圆环(阴影部分),为求该圆环的面积,只需测量一条线段的长度,这条线段就是( )