题目内容
7.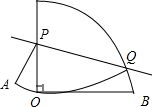 如图,是一个圆心角为90°的扇形,AO=2cm,点P在半径AO上运动,点Q在弧AB上运动,沿PQ将它以上的部分向下翻折,使翻折后的弧恰好过点O,则OP的最大距离为$\frac{2\sqrt{3}}{3}$.
如图,是一个圆心角为90°的扇形,AO=2cm,点P在半径AO上运动,点Q在弧AB上运动,沿PQ将它以上的部分向下翻折,使翻折后的弧恰好过点O,则OP的最大距离为$\frac{2\sqrt{3}}{3}$.
分析 作O关于PQ的对称点O′,O′恰好落在⊙O上,于是得到OP=$\frac{\frac{1}{2}R}{cos∠POE}$,推出△OO′Q为等边三角形,根据等边三角形的性质得到OQ=O′Q=OO′=R,当cos∠POE最小时,∠POE最大,当∠QOB=0°时,∠POE=30°于是得到结论.
解答 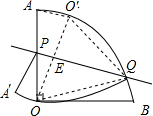 解:作O关于PQ的对称点O′,O′恰好落在⊙O上,
解:作O关于PQ的对称点O′,O′恰好落在⊙O上,
∴OP=$\frac{\frac{1}{2}R}{cos∠POE}$,
∵△OO′Q为等边三角形,
∴OQ=O′Q=OO′=R,∠POE+∠QOB=30°,
当cos∠POE最小时,∠POE最大,
当∠QOB=0°时,∠POE=30°,
∴OP=$\frac{1}{cos30°}$=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查了翻折变换-折叠问题,等边三角形的判定和性质,正确的在才辅助线是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 已知:如图,正方形ABCD的边长为6,BM,DN分别平分正方形的两个外角,且满足∠MAN=45°,连接MC,NC,MN.
已知:如图,正方形ABCD的边长为6,BM,DN分别平分正方形的两个外角,且满足∠MAN=45°,连接MC,NC,MN. 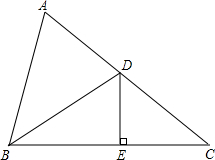 如图:△ABC中,BA=BD,DE垂直平分BC,∠ABD=40°,则∠C=35°.
如图:△ABC中,BA=BD,DE垂直平分BC,∠ABD=40°,则∠C=35°. 如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,若AC=9cm,BC=5cm,则△BCE的周长为14cm.
如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,若AC=9cm,BC=5cm,则△BCE的周长为14cm.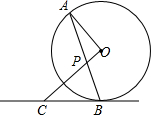 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的⊙O的切线交OP的延长线于点C.
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的⊙O的切线交OP的延长线于点C.