题目内容
2．若a＞5，那么（5-a）x＞a-5的解集为x＜-1．分析 由a＞5可得a-5＞0，即5-a＜0，根据性质3将不等式系数化为1可得．
解答 解：∵a＞5，
∴5-a＜0，
∴不等式（5-a）x＞a-5两边同时除以5-a，
得：x＜$\frac{a-5}{5-a}$=-1，即x＜-1，
故答案为：x＜-1．
点评 本题考查了不等式的解法，熟练掌握不等式的基本性质是解不等式的根本依据．
练习册系列答案
相关题目
12．已知∠AOB=32°，射线OC⊥OA，则∠COB的度数为（ ）
| A． | 122° | B． | 58° | ||
| C． | 122°或58° | D． | 以上答案均不正确 |
17．某工厂为了对新研发的一种产品进行合理定价，将该产品按拟定的价格进行试销，通过对5天的试销情况进行统计，得到如下数据：
（1）通过对上面表格中的数据进行分析，发现销量y（件）与单价x（元/件）之间存在一次函数关系，求y关于x的函数关系式（不需要写出函数自变量的取值范围）；
（2）预计在今后的销售中，销量与单价仍然存在（2）中的关系，且该产品的成本是20元/件．为使工厂获得最大利润，该产品的单价应定为多少？
（3）为保证产品在实际试销中销售量不得低于30件，且工厂获得得利润不得低于400元，请直接写出单价x的取值范围．
| 单价（元/件） | 30 | 34 | 38 | 40 | 42 |
| 销量（件） | 40 | 32 | 24 | 20 | 16 |
（2）预计在今后的销售中，销量与单价仍然存在（2）中的关系，且该产品的成本是20元/件．为使工厂获得最大利润，该产品的单价应定为多少？
（3）为保证产品在实际试销中销售量不得低于30件，且工厂获得得利润不得低于400元，请直接写出单价x的取值范围．
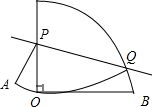如图，是一个圆心角为90°的扇形，AO=2cm，点P在半径AO上运动，点Q在弧AB上运动，沿PQ将它以上的部分向下翻折，使翻折后的弧恰好过点O，则OP的最大距离为$\frac{2\sqrt{3}}{3}$．
如图，若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点，且OC=3BD．则实数k的值为$\frac{9\sqrt{3}}{4}$．
如图，在△ABC中，BA=BC=20cm，AC=30cm，点P从A出发，沿AB以4cm/s的速度向点B运动；同时点Q从C点出发，沿CA以3cm/s的速度向A点运动．设运动时间为x（s）．