Question

5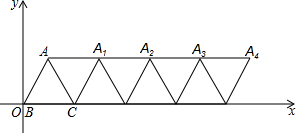．如图，在平面直角坐标系内，边长为4的等边△ABC的顶点B与原点重合，将△ABC绕顶点C顺时针旋转60°的△ACA₁，将四边形ABCA₁看作一个基本图形，将此基本图形不断复制并平移，则A₂₀₁₇的坐标为（8070，2$\sqrt{3}$）．

Answer 1

分析 根据等边三角形的性质易得OA=BC=4，∠AOC=60°．过点A作AD⊥x轴于D，求出BD=DC=$\frac{1}{2}$BC=2，AD=OA•sin∠AOD=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$，那么A（2，2$\sqrt{3}$）．再利用旋转与平移的性质分别求出A₁（2+4，2$\sqrt{3}$），A₂（2+4×2，2$\sqrt{3}$），A₃（2+4×3，2$\sqrt{3}$），依此类推即可求出A₂₀₁₇的坐标．

解答 解：∵边长为4的等边△ABC的顶点B与原点重合，
∴OA=BC=4，∠AOC=60°，
如图，过点A作AD⊥x轴于D，
∴BD=DC=$\frac{1}{2}$BC=2，AD=OA•sin∠AOD=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$，
∴A（2，2$\sqrt{3}$）．
∵将△ABC绕顶点C顺时针旋转60°的△ACA₁，
∴四边形AOCA₁是平行四边形，
∴AA₁=OC=4，AA₁∥OC，
∴A₁（2+4，2$\sqrt{3}$），即A₁（6，2$\sqrt{3}$）；
∵将四边形ABCA₁看作一个基本图形，将此基本图形不断复制并平移，
∴A₂（2+4×2，2$\sqrt{3}$），即A₂（10，2$\sqrt{3}$）；
A₃（2+4×3，2$\sqrt{3}$），即A₃（14，2$\sqrt{3}$）；
…
∴A₂₀₁₇的坐标为（2+4×2017，2$\sqrt{3}$），即A₂₀₁₇（8070，2$\sqrt{3}$）；
故答案为（8070，2$\sqrt{3}$）．

点评 本题考查了等边三角形的性质，旋转与平移的性质，正确求出A₁，A₂，A₃的坐标从而找出规律是解题的关键．