题目内容
2.在Rt△ABC中,∠C=90°,∠B=70°,点D在边AB上,△ABC绕点D旋转后点B与点C重合,点C落在点C′,那么∠ACC′的度数是50°.
分析 先根据DB=DC,∠B=70°,∠ACB=90°,即可得到∠BCD=70°,∠ACD=90°-70°=20°,再根据旋转可得,∠B=∠A'CC'=70°,最后求得∠ACC'=70°-20°=50°.
解答  解:如图所示,∵△ABC绕点D旋转后点B与点C重合,
解:如图所示,∵△ABC绕点D旋转后点B与点C重合,
∴DB=DC,
又∵∠B=70°,∠ACB=90°,
∴∠BCD=70°,∠ACD=90°-70°=20°,
由旋转可得,∠B=∠A'CC'=70°,
∴∠ACC'=70°-20°=50°.
故答案为:50°.
点评 本题主要考查了旋转的性质的运用,解题时注意:对应点与旋转中心所连线段的夹角等于旋转角,旋转前、后的图形全等.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
12.为了解某校八、九年级部分学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如图的统计图表:
睡眠情况分段情况如下
根据图表提供的信息,回答下列问题:
(Ⅰ)直接写出统计图中a的值5%;
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?
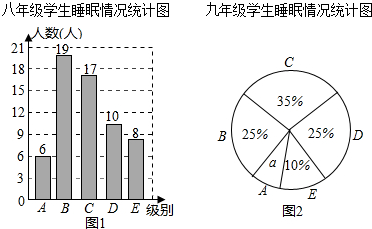
睡眠情况分段情况如下
| 组别 | 睡眠时间x(小时) |
| A | 4.5≤x<5.5 |
| B | 5.5≤x<6.5 |
| C | 6.5≤x<7.5 |
| D | 7.5≤x<8.5 |
| E | 8.5≤x<9.5 |
(Ⅰ)直接写出统计图中a的值5%;
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?

17.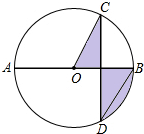 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分图形的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分图形的面积为( )
 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分图形的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分图形的面积为( )| A. | 4π | B. | 2π | C. | π | D. | $\frac{2π}{3}$ |
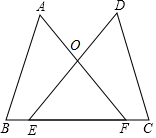 已知:如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
已知:如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.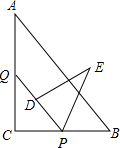 如图,在Rt△ABC中,∠C=90°,AB=15,BC=9.点P、Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
如图,在Rt△ABC中,∠C=90°,AB=15,BC=9.点P、Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上. 如图,从电线杆离地面9m处向地面拉一条长15m的固定缆绳,这条缆绳在地面的固定点距离电线杆底部有12m.
如图,从电线杆离地面9m处向地面拉一条长15m的固定缆绳,这条缆绳在地面的固定点距离电线杆底部有12m.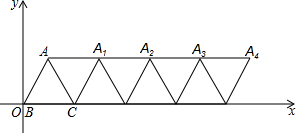 如图,在平面直角坐标系内,边长为4的等边△ABC的顶点B与原点重合,将△ABC绕顶点C顺时针旋转60°的△ACA1,将四边形ABCA1看作一个基本图形,将此基本图形不断复制并平移,则A2017的坐标为(8070,2$\sqrt{3}$).
如图,在平面直角坐标系内,边长为4的等边△ABC的顶点B与原点重合,将△ABC绕顶点C顺时针旋转60°的△ACA1,将四边形ABCA1看作一个基本图形,将此基本图形不断复制并平移,则A2017的坐标为(8070,2$\sqrt{3}$).