题目内容
17．
如图，在Rt△ABC中，∠C=90°，∠A=30°，D为AB中点，DE⊥AC于E，AB=8，则DE的长度为（ ）| A． | 1 | B． | 2 | C． | 4 | D． | 8 |
分析 根据D为AB的中点可求出AD的长，再根据在直角三角形中，30°角所对的直角边等于斜边的一半即可求出DE的长度．
解答 解：∵D为AB的中点，AB=8，
∴AD=4，
∵DE⊥AC于点E，∠A=30°，
∴DE=$\frac{1}{2}$AD=2，
故选：B．
点评 本题考查了直角三角形的性质：直角三角形中，30°角所对的直角边等于斜边的一半．
练习册系列答案
智慧小复习系列答案
相关题目
8．下列四幅图∠1和∠2是同位角的是（ ）
| A． | ①② | B． | ②④ | C． | ①③ | D． | ①④ |
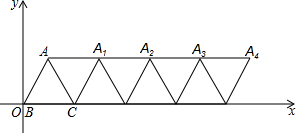如图，在平面直角坐标系内，边长为4的等边△ABC的顶点B与原点重合，将△ABC绕顶点C顺时针旋转60°的△ACA1，将四边形ABCA1看作一个基本图形，将此基本图形不断复制并平移，则A2017的坐标为（8070，2$\sqrt{3}$）．
12．
如图，?ABCD的对角线AC与BD相交于点O，AB⊥AC，若AB=4，∠ACB=30°，则BD的长是（ ）
如图，?ABCD的对角线AC与BD相交于点O，AB⊥AC，若AB=4，∠ACB=30°，则BD的长是（ ）| A． | 2$\sqrt{3}$ | B． | 2$\sqrt{7}$ | C． | 4$\sqrt{3}$ | D． | 4$\sqrt{7}$ |
如图，△ABC的三个顶点的坐标分别为A（-3，5），B（-3，0），C（2，0），将△ABC绕点B顺时针旋转一定角度后使A落在y轴上，与此同时顶点C恰好落在y=$\frac{k}{x}$的图象上，则k的值为（ ）
如图，在平面直角坐标系xOy中，直线y=-$\frac{3}{4}$x+3与x轴，y轴分别交于点A、B，点C的坐标为（0，-2），若点D在直线AB上运动，点E在直线AC上运动，当以O、A、D、E为顶点的四边形是平行四边形时，点D的坐标为（$\frac{12}{5}$，$\frac{6}{5}$）或（$\frac{28}{5}$，-$\frac{6}{5}$）．