题目内容
9.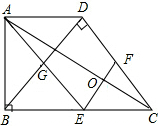 已知:在梯形ABCD中.AD∥BC,∠ABC=90°,∠BDC=90°,BC=2AD,E,F分别是BC、DC的中点.连接AE、EF、AC,连接BD,交AE于点G.
已知:在梯形ABCD中.AD∥BC,∠ABC=90°,∠BDC=90°,BC=2AD,E,F分别是BC、DC的中点.连接AE、EF、AC,连接BD,交AE于点G.求证:四边形EFDG是正方形.
分析 欲证明四边形EFDG是正方形,只需证得四边形EFDG是矩形,然后推知GD=DE,即可得四边形EFDG是正方形.
解答 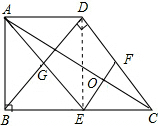 证明:连接DE,
证明:连接DE,
∵E、F分别是BC、CD的中点,
∴EF∥BD,
∵四边形AECD是平行四边形,
∴AE∥DC,
∴四边形EFDG是平行四边形,
又∠BDC=90°,
∴四边形EFDG是矩形.
∵AD∥BE且AD=BE,
∴四边形ABED是平行四边形,
又∵∠ABE=90°,
∴平行四边形ABED是矩形,
∴AE=BD,
∴GD=GE,
∴平行四边形EFDG是正方形.
点评 此题考查了平行四边形的判定与性质、矩形的判定与性质以及正方形的判定与性质.此题难度适中,注意辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
4.已知抛物线y=-(x-m)2的顶点为A,直线l:y=$\sqrt{3}$x-$\sqrt{3}$m,其中m>0
(1)求抛物线的对称轴及点A的坐标(用含m的代数式表示);
(2)证明:点A在直线l上.
(1)求抛物线的对称轴及点A的坐标(用含m的代数式表示);
(2)证明:点A在直线l上.
4.有一个多边形,它的内角和等于它的外角和的2倍,则它是( )
| A. | 三边形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
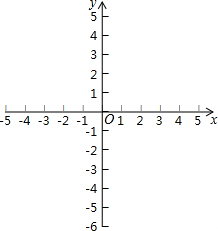 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-4(m≠0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴交于点D.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-4(m≠0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴交于点D.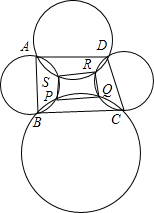 若以圆内接四边形ABCD的各边为弦作任意圆,求证:这些圆相交的四点共圆.
若以圆内接四边形ABCD的各边为弦作任意圆,求证:这些圆相交的四点共圆.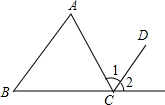 已知:如图,AB∥CD,若∠A=66°∠B=45°,则∠1=66°,∠2=45°.
已知:如图,AB∥CD,若∠A=66°∠B=45°,则∠1=66°,∠2=45°. 如图,直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解.观察该图回答:直线l与m的交点M的坐标为(1,1).方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
如图,直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解.观察该图回答:直线l与m的交点M的坐标为(1,1).方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$. 已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.