题目内容
15.如图,点O是平面直角坐标系的原点,点A的坐标为(0,6),以A为顶点的抛物线交x轴于B点,其中 点B在x轴正半轴上,连接AB,以 AB为边作矩形ABCD交y轴于点C(按顺时针方向标记),矩形ABCD随着点B位置的变化而随之相应变化.(1)若矩形ABCD为正方形,求抛物线的函数关系式;
(2)在点B位置变化的过程中,点D的落点在(1)中的抛物线上吗?如果在,请证明;如果不在,请说明理由;并求出OD的最小值;
(3)若点M(-3,-3)落在矩形ABCD的边AD上,求出D点坐标.
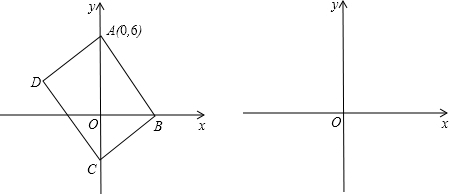
分析 (1)由正方形的性质可求得B(6,0),设抛物线的解析式为y=ax2+6,将点B的坐标代入得可求得a的值,从而得到抛物线的坐标;
(2)如图1所示:过点D作DE⊥AC,垂足为E.设点B的坐标为(a,0)a>0.然后依据待定系数法求得AB的解析式(含a的式子),然后再依据待定系数法求得BC的解析式(含a的式子),于是可求得点C的坐标为(0,-$\frac{{a}^{2}}{6}$),接下来,证明△ADE≌△CBO,可得到点D的坐标,从而可证明点D在抛物线上;
(3)先求得直线AM的解析式,然后由点D在AM上,可设点D的坐标为(a,3a+6),将点D的坐标代入y=-$\frac{1}{6}$x2+6求得a的值,从而可求得点D的坐标.
解答 解:(1)∵四边形ABCD为正方形,
∴∠CAB=45°.
又∵∠AOB=90°,
∴∠ABO=45°.
∴OA=OB.
∴点B的坐标为(6,0).
设抛物线的解析式为y=ax2+6.
∵将点B的坐标代入得36a+6=0,解得:a=-$\frac{1}{6}$,
∴抛物线的解析式为y=-$\frac{1}{6}$x2+6.
(2)如图1所示:过点D作DE⊥AC,垂足为E.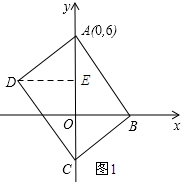
设点B的坐标为(a,0)a>0.
设直线AB的解析式为y=kx+6.
∵将B(a,0)代入抛物线的解析式得:ak+6=0,解得;k=-$\frac{6}{a}$,
∴直线AB的解析式为y=-$\frac{6}{a}$x+6.
∵BC⊥AB,
∴直线BC的一次项系数为$\frac{a}{6}$.
设直线BC的解析式为y=$\frac{a}{6}$x+c.
∵将点B的坐标(a,0)代入得:$\frac{{a}^{2}}{6}$+c=0,解得:c=$-\frac{{a}^{2}}{6}$,
∴直线BC的解析式为y=$\frac{a}{6}x$-$\frac{{a}^{2}}{6}$.
∵当x=0时,y=-$\frac{{a}^{2}}{6}$,
∴点C的坐标为(0,-$\frac{{a}^{2}}{6}$).
∵ABCD为矩形,
∴AD=BC,AD∥BC.
∴∠DAE=∠BCO.
∵DE⊥AC,
∴∠DEA=90°.
在△ADE和△CBO中,
$\left\{\begin{array}{l}{∠DAE=∠BCO}\\{∠DEA=∠BOC}\\{AD=BC}\end{array}\right.$,
∴DE=OB,OC=AE.
∴点D的坐标为(-a,6-$\frac{{a}^{2}}{6}$).
∵将x=-a代入y=-$\frac{1}{6}$x2+6得:y=$-\frac{1}{6}$a2+6,
∴点D在抛物线y=-$\frac{1}{6}$x2+6上.
(3)设AM的解析式为y=kx+b.
∵将点A、M的坐标代入得:$\left\{\begin{array}{l}{b=6}\\{-3k+b=-3}\end{array}\right.$,解得:k=3,b=6,
∴直线AM的解析式为y=3x+6.
设点D的坐标为(a,3a+6),将点D的坐标代入y=-$\frac{1}{6}$x2+6得:-$\frac{1}{6}$a2+6=3a+6,
解得:a=-18,a=0(舍去).
∴点D的坐标为(-18,-48).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式,一次函数的解析式,点的坐标与函数解析式的关系,明确相互垂直的两条直线的一次项系数的乘积为-1是解题的关键.

 如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )
如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
 如图为一个正方体的表面展开图,则该正方体的六个表面中,与“善”字相对的面上的字是( )
如图为一个正方体的表面展开图,则该正方体的六个表面中,与“善”字相对的面上的字是( )| A. | 敬 | B. | 业 | C. | 诚 | D. | 信 |
| A. | 三边形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-4(m≠0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴交于点D.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-4(m≠0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴交于点D. 如图,直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解.观察该图回答:直线l与m的交点M的坐标为(1,1).方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
如图,直线l上所有点的坐标都是方程x+y=2的解,直线m上所有点的坐标都是方程x-y=0的解.观察该图回答:直线l与m的交点M的坐标为(1,1).方程组$\left\{\begin{array}{l}{x+y=2}\\{x-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$. 已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.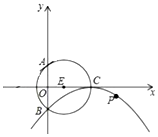 如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=kx+4k+1(k为实数),以点C为顶点的抛物线过点B.
如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=kx+4k+1(k为实数),以点C为顶点的抛物线过点B.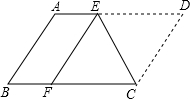 如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AB上.
如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AB上.