Question

13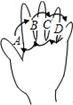．如图为手的示意图，在各个手指间标记字母A，B，C，D．请你按图中箭头所指方向（即A→B→C→D→C→B→A→B→C→…的方式）从A开始数连续的正整数1，2，3，4，…，当字母B第（2n-1）次出现时（n为正整数），恰好数到的数是6n-4（用含n的代数式表示）．

Answer 1

分析 设字母B第n次出现时，数到的数是a_n（n为正整数），根据数数规律写出部分a_n的值，根据数的变化找出变化规律“a_2n-1=6n-4，a_2n=6n”，依此规律即可得出结论．

解答 解：设字母B第n次出现时，数到的数是a_n（n为正整数），
观察，发现规律：a₁=2，a₂=6，a₃=8，a₄=12，…，
∴a_2n-1=6n-4，a_2n=6n．
故答案为：6n-4．

点评 本题考查了规律型中的数字的变换类，解题的关键是找出变换规律“a_2n-1=6n-4，a_2n=6n”．本题属于基础题，难度不大，解决该题型题目时，写出部分a_n的值，根据数的变化找出变化规律是关键．