��Ŀ����
5�� ��ͼ���ھ���ABCD�У�BC=10��AB=4������E�ӵ�B������BC���յ�C��ÿ��1����λ���ȵ��ٶ��˶�������F������BA-AD���յ�D��ÿ��2����λ���ȵ��ٶ��˶�������E��BF��ƽ���������F��BE��ƽ�����ཻ�ڵ�G������E��Fͬʱ����������һ���㵽���յ�ʱ����һ��������˶�ֱ�������յ�ֹͣ���ı���BEGF�����ABCD�ص����ֵ����ΪS��ƽ����λ�����˶���ʱ��Ϊt���룩��
��ͼ���ھ���ABCD�У�BC=10��AB=4������E�ӵ�B������BC���յ�C��ÿ��1����λ���ȵ��ٶ��˶�������F������BA-AD���յ�D��ÿ��2����λ���ȵ��ٶ��˶�������E��BF��ƽ���������F��BE��ƽ�����ཻ�ڵ�G������E��Fͬʱ����������һ���㵽���յ�ʱ����һ��������˶�ֱ�������յ�ֹͣ���ı���BEGF�����ABCD�ص����ֵ����ΪS��ƽ����λ�����˶���ʱ��Ϊt���룩����1����tΪ��ֵʱ����G���D�غϣ�
��2�����ı���BEGF�����ABCD �ص����ֵ�ͼ�����ı���ʱ����S��t�ĺ�����ϵʽ��
��3�����˶������У�����CEG�ǵ���������ʱ��ֱ��д��t��ֵ��
���� ��1������AF+FD=10�г����̼��ɽ�����⣮
��2�����������ηֱ����ٵ�0��t��2ʱ���ڵ�2��t$��\frac{14}{3}$ʱ���۵�7��t��10ʱ���ֱ���⼴�ɣ�
��3����CEG�ǵ���������ʱ���֡�C����E����G�ǵ��������εĶ��ǽ������ۣ�ע���CΪ����ʱҲ���������Σ�
��� �⣺��1�������⣺��2t-4��+t=10�����t=$\frac{14}{3}$��
��2����0��t��2ʱ��S=2t2��
��2��t$��\frac{14}{3}$ʱS=4t��
��7��t��10ʱ��S=$\frac{1}{2}$��4��10-$\frac{1}{2}$����10-t��2��$\frac{2}{5}$=-$\frac{1}{5}$t2+4t��
��3����CG=CEʱ����ͼ1�У�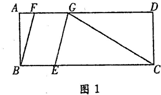
��CG2=CD2+DG2=42+��14-3t��2��EC2=��10-t��2��
�ࣨ10-t��2=42+��14-3t��2��
���t=4-$\sqrt{2}$��4+$\sqrt{2}$����������
��EG=CGʱ����ͼ2�У�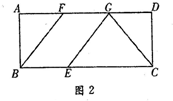
���ı���BFGE��ƽ���ı��Σ�
��BF=GE=GC����AB=CD��
��AF=DG��
��2t-4=14-3t��
��t=$\frac{18}{5}$��
��EC=EGʱ����ͼ3��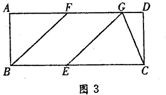
��EG2=BF2=AB2+AF2��EC2=��10-t��2
�ࣨ10-t��2=42+��2t-4��2��
���t=$\frac{-2+4\sqrt{13}}{3}$��$\frac{-2-4\sqrt{13}}{3}$����������
��CG=CEʱ����ͼ4�У�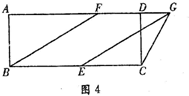
��CG2=CD2+DG2=42+��3t-14��2��
EC2=��10-t��2
�ࣨ10-t��2=42+��3t-14��2��
���t=4+$\sqrt{2}$��4-$\sqrt{2}$����������
�൱��CEG�ǵ���������ʱ��t=4-$\sqrt{2}$��4+$\sqrt{2}$��$\frac{18}{5}$��$\frac{-2+4\sqrt{13}}{3}$��
���� ���⿼���ı����ۺ��⡢���ε����ʡ����ɶ�����֪ʶ������Ĺؼ�����ȷ����ͼ�Σ�ѧ���÷��̵�˼��˼�����⣬ע�����һ�����Σ�����©�⣬�����п�ѹ����

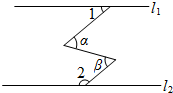 ��ͼ��ֱ��l1��l2���Ϧ�=�Ϧ£���1=40�㣬���2=��������
��ͼ��ֱ��l1��l2���Ϧ�=�Ϧ£���1=40�㣬���2=��������| A�� | 100�� | B�� | 120�� | C�� | 140�� | D�� | 160�� |
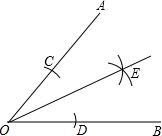 �۲�ͼ�г߹���ͼ�ۼ�������˵��������ǣ�������
�۲�ͼ�г߹���ͼ�ۼ�������˵��������ǣ�������| A�� | OE�ǡ�AOB��ƽ���� | B�� | OC=OD | ||
| C�� | ��C��D��OE�ľ��벻��� | D�� | ��AOE=��BOE |
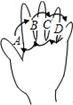 ��ͼΪ�ֵ�ʾ��ͼ���ڸ�����ָ������ĸA��B��C��D�����㰴ͼ�м�ͷ��ָ����A��B��C��D��C��B��A��B��C�����ķ�ʽ����A��ʼ��������������1��2��3��4����������ĸB�ڣ�2n-1���γ���ʱ��nΪ����������ǡ������������6n-4���ú�n�Ĵ���ʽ��ʾ����
��ͼΪ�ֵ�ʾ��ͼ���ڸ�����ָ������ĸA��B��C��D�����㰴ͼ�м�ͷ��ָ����A��B��C��D��C��B��A��B��C�����ķ�ʽ����A��ʼ��������������1��2��3��4����������ĸB�ڣ�2n-1���γ���ʱ��nΪ����������ǡ������������6n-4���ú�n�Ĵ���ʽ��ʾ����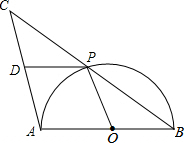 ��ͼ��AB�ǰ�ԲO��ֱ������P�ǰ�Բ�ϲ����A��B�غϵ�һ�����㣬�ӳ�BP����C��ʹPC=PB��D��AC���е㣬����PD��PO��
��ͼ��AB�ǰ�ԲO��ֱ������P�ǰ�Բ�ϲ����A��B�غϵ�һ�����㣬�ӳ�BP����C��ʹPC=PB��D��AC���е㣬����PD��PO��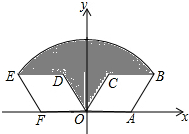 ��ͼ������OABC�Ķ���A������Ϊ��2��0������COA=60�㣬������OABC������ԭ��O��ʱ����ת120��õ�����ODEF����ͼ����Ӱ���ֵ����Ϊ4��-2$\sqrt{3}$��
��ͼ������OABC�Ķ���A������Ϊ��2��0������COA=60�㣬������OABC������ԭ��O��ʱ����ת120��õ�����ODEF����ͼ����Ӱ���ֵ����Ϊ4��-2$\sqrt{3}$�� ����y=$\frac{4}{x}$��y=$\frac{1}{x}$�ڵ�һ�����ڵ�ͼ����ͼ��ʾ����P��y=$\frac{4}{x}$��ͼ����һ���㣬��PC��x���ڵ�C����y=$\frac{1}{x}$��ͼ���ڵ�A����PD��y���ڵ�D����y=$\frac{1}{x}$��ͼ���ڵ�B���������½��ۣ��١�ODB���OCA�������ȣ���PA��PBʼ����ȣ����ı���PAOB�������С���ᷢ���仯����PA=3AC��������ȷ�Ľ�������ǣ�������
����y=$\frac{4}{x}$��y=$\frac{1}{x}$�ڵ�һ�����ڵ�ͼ����ͼ��ʾ����P��y=$\frac{4}{x}$��ͼ����һ���㣬��PC��x���ڵ�C����y=$\frac{1}{x}$��ͼ���ڵ�A����PD��y���ڵ�D����y=$\frac{1}{x}$��ͼ���ڵ�B���������½��ۣ��١�ODB���OCA�������ȣ���PA��PBʼ����ȣ����ı���PAOB�������С���ᷢ���仯����PA=3AC��������ȷ�Ľ�������ǣ�������