题目内容
4. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.(1)求证:CB∥PD;
(2)若BC=6,sin∠P=$\frac{2}{5}$,求AB的值.
分析 (1)根据∠1=∠C及圆周角定理可得出∠1=∠P,由此可得出结论;
(2)连接AC,根据圆周角定理得出∠ACB=90°,再由垂径定理得出$\widehat{BC}$=$\widehat{BD}$,故可得出∠P=∠CAB,根据锐角三角函数的定义即可得出结论.
解答  (1)证明:∵∠1=∠C,∠C=∠P,
(1)证明:∵∠1=∠C,∠C=∠P,
∴∠1=∠P,
∴CB∥PD.
(2)解:连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°.
∵CD⊥AB,
∴$\widehat{BC}$=$\widehat{BD}$,
∴∠P=∠CAB,
∴sin∠CAB=$\frac{BC}{AB}$=$\frac{2}{5}$.
∵BC=6,
∴AB=15.
点评 本题考查的是圆周角定理,根据题意作出辅助线,构造出圆周角是解答此题的关键.

练习册系列答案
相关题目
2.不等式2x>-3解集是( )
| A. | x>-$\frac{2}{3}$ | B. | x<-$\frac{2}{3}$ | C. | x>-$\frac{3}{2}$ | D. | x<-$\frac{3}{2}$ |
3.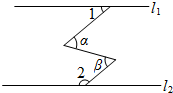 如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=( )
如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=( )
 如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=( )
如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=( )| A. | 100° | B. | 120° | C. | 140° | D. | 160° |
16.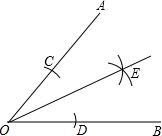 观察图中尺规作图痕迹,下列说法错误的是( )
观察图中尺规作图痕迹,下列说法错误的是( )
 观察图中尺规作图痕迹,下列说法错误的是( )
观察图中尺规作图痕迹,下列说法错误的是( )| A. | OE是∠AOB的平分线 | B. | OC=OD | ||
| C. | 点C、D到OE的距离不相等 | D. | ∠AOE=∠BOE |
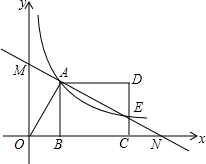 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.
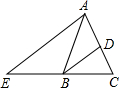 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠BAC=40°,请你选择图中现有的一个角并求出它的度数(要求:不添加新的线段,所有给出的条件至少使用一次).
如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠BAC=40°,请你选择图中现有的一个角并求出它的度数(要求:不添加新的线段,所有给出的条件至少使用一次).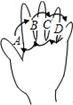 如图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4,…,当字母B第(2n-1)次出现时(n为正整数),恰好数到的数是6n-4(用含n的代数式表示).
如图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4,…,当字母B第(2n-1)次出现时(n为正整数),恰好数到的数是6n-4(用含n的代数式表示). 函数y=$\frac{4}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P是y=$\frac{4}{x}$的图象上一动点,作PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,作PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( )
函数y=$\frac{4}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P是y=$\frac{4}{x}$的图象上一动点,作PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,作PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( )