题目内容
11.关于x的一元二次方程|m|x2-2x+1=0有两个不相等的实数根,则m的取值范围是( )| A. | -1<m<1 | B. | -1<m<1且m≠0 | C. | m>1 | D. | m<1且m≠0 |
分析 根据方程有两个不相等的实数根可得△=(-2)2-4|m|>0,由一元二次方程的定义可得m≠0,解不等式知m的取值范围.
解答 解:∵关于x的一元二次方程|m|x2-2x+1=0有两个不相等的实数根,
∴△=(-2)2-4|m|>0,即4-4|m|>0,且m≠0,
解得:-1<m<1,且m≠0,
故选:B.
点评 本题主要考查一元二次方程的定义及根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;
②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
1.tan45°的值等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
2.不等式2x>-3解集是( )
| A. | x>-$\frac{2}{3}$ | B. | x<-$\frac{2}{3}$ | C. | x>-$\frac{3}{2}$ | D. | x<-$\frac{3}{2}$ |
19.在“纪念抗日战争胜利暨世界反法西斯战争胜利70周年”歌咏比赛中,10位评委给小红的评分情况如表所示:
则下列说法正确的是( )
| 成绩(分) | 6 | 7 | 8 | 9 | 10 |
| 人数 | 3 | 2 | 3 | 1 | 1 |
| A. | 中位数是7.5分 | B. | 中位数是8分 | C. | 众数是8分 | D. | 平均数是8分 |
6.方程2x2-6x+3=0的根的情况是( )
| A. | 有两个同号的不相等的实数根 | B. | 有两个异号的不相等的实数根 | ||
| C. | 有两个相等的实数根 | D. | 没有实数根 |
16.一个圆锥的侧面展开图是一个半径为5的半圆,则该圆锥的底面半径为( )
| A. | 2.5 | B. | 5 | C. | 2.5π | D. | 5π |
3.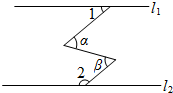 如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=( )
如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=( )
 如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=( )
如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=( )| A. | 100° | B. | 120° | C. | 140° | D. | 160° |
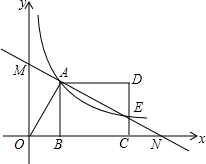 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.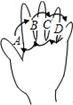 如图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4,…,当字母B第(2n-1)次出现时(n为正整数),恰好数到的数是6n-4(用含n的代数式表示).
如图为手的示意图,在各个手指间标记字母A,B,C,D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4,…,当字母B第(2n-1)次出现时(n为正整数),恰好数到的数是6n-4(用含n的代数式表示).