��Ŀ����
17����֪����y=-x+4��ͼ���뺯��$y=\frac{k}{x}$��ͼ����ͬһ����ϵ�ڣ�����y=-x+4��ͼ����ͼ1�������ύ��A��B���㣬��M��2��m����ֱ��AB��һ�㣬��N���M����y��Գƣ��߶�MN��y���ڵ�C����1��m=2��S��AOB=8��
��2������߶�MN������������$y=\frac{k}{x}$��ͼ��ֳ������֣������������ֳ��ȵı�Ϊ1��3����k��ֵ��
��3����ͼ2��������������$y=\frac{k}{x}$ͼ����N����ʱ�����������ϴ���������E��x1��y1����F��x2��y2������ԭ��Գ��ҵ�ֱ��MN�ľ���֮��Ϊ1��3����x1��x2��ֱ��д������������꣮
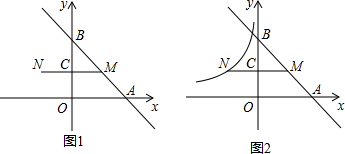
���� ��1�����õ��ں���ͼ���ϵ��ص����m���Լ�ƽ��ֱ������ϵ�������ε�����ļ��㷽���������������ƽ�����������ֱ���ϵı���Ϊ�ף���
��2�����õ�ĶԳƵ�������ص����N������꣬�߶�MN������������$y=\frac{k}{x}$��ͼ��ֳ������֣������������ֳ��ȵı�Ϊ1��3���ҽ���ΪD�����������$\frac{ND}{DM}=\frac{1}{3}$��$\frac{ND}{DM}=\frac{3}{1}$���㼴�ɣ�
��3�����õ㵽ƽ�����������ֱ�ߵľ���ļ��㷽���Լ��ͣ�2�����Ƶķ������������������ȡ����ֵʱ��ҲҪ��������㣮
��� �⣺��1����M��2��m����ֱ��y=-x+4��ͼ���ϣ�
��m=-2+4=2��
����y=-x+4��ͼ���������ύ��A��B���㣬
��A��4��0����B��0��4����
��OA=4��OB=4��
��S��AOB=$\frac{1}{2}$OA��OB=$\frac{1}{2}$��4��4=8��
�ʴ�Ϊ2��8��
��2����m=2��
��M��2��2����
�ߵ�N���M����y��Գƣ�
��N��-2��2����
��MN=4��
���߶�MN������������$y=\frac{k}{x}$��ͼ��ֳ������֣������������ֳ��ȵı�Ϊ1��3���ҽ���ΪD��
�ٵ�$\frac{ND}{DM}=\frac{1}{3}$ʱ������$\frac{ND}{MN}=\frac{1}{4}$��
��ND=1��
��D��-1��2����
��k=-1��2=-2��
�ڵ�$\frac{ND}{DM}=\frac{3}{1}$ʱ������$\frac{MN}{DM}=\frac{4}{1}$��
��DM=$\frac{1}{4}$MN=$\frac{1}{4}$��4=1��
��D��1��2����
��k=1��2=2��
��k��ֵΪ-2��2��
��3������������$y=\frac{k}{x}$ͼ����N����N��-2��2����
��k=-2��2=-4��
�߷����������ϴ���������E��x1��y1����F��x2��y2����
��x1y1=-4x2��y2=-4��
�ߵ�E��x1��y1����F��x2��y2������ԭ��Գƣ�
��x2=-x1��y2=-y1��
��M��2��2����N��-2��2����
���E��ֱ��MN�ľ���Ϊ|y1-2|����F��ֱ��MN�ľ���Ϊ|y1+2|��
�ߵ�E��x1��y1����F��x2��y2����ֱ��MN�ľ���֮��Ϊ1��3��
���E��x1��y1����F��-x1��-y1����ֱ��MN�ľ���֮��Ϊ1��3��
�ٵ�$\frac{{|y}_{1}-2|}{{|y}_{1}+2|}=\frac{1}{3}$ʱ������3|y1-2|=|y1+2|
��y1��2ʱ��3y1-6=y1+2��
��y1=4��
��y2=-4��x1=-1��x2=1
��-2��y1��2ʱ��-3y1+6=y1+2��
��y1=1��
��y2=-1��x1=-4��x2=4
��y1��-2ʱ��-3y1+6=-y1+2��
��y1=2���ᣩ��
�ڵ�$\frac{{|y}_{1}-2|}{{|y}_{1}+2|}=\frac{3}{1}$ʱ������3|y1+2|=|y1-2|��
��y1��2ʱ��3y1+6=y1-2��
��y1=-4���ᣩ��
��-2��y1��2ʱ��3y1+6=-y1+2��
��y1=-1��
��y2=1��x1=4��x2=-4����x1��x2���ᣩ��
��y1��-2ʱ��-3y1-6=-y1+2��
��y1=-4��
��y2=4��x1=1��x2=-1����x1��x2���ᣩ��
��E��-1��4����F��1��-4����E��-4��1����F��4��-1��
���� �����Ƿ�����������һ���ۺ��⣬��Ҫ�����˵��ں���ͼ���ϵ��ص㣬�����m������ϵ�м�������������ķ�������������������֮��ľ���͵㵽ֱ�ߵľ��룬�����ND��MD����E��F��ֱ��MN�ľ��룬����Ĺؼ���ȷ��ȷ������ľ���͵㵽ֱ�ߵľ����ȷ�������õ��˷ּ���������㣬��������һ�������

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | x��-1 | B�� | x��-1 | C�� | x��-1 | D�� | x��-1 |
 ��ͼ��Բ�ڽ��ı���ABCD������Աߵ��ӳ��߷ֱ�����ڵ�E��F������A=55�㣬��E=30�㣬���F=��������
��ͼ��Բ�ڽ��ı���ABCD������Աߵ��ӳ��߷ֱ�����ڵ�E��F������A=55�㣬��E=30�㣬���F=��������| A�� | 25�� | B�� | 30�� | C�� | 40�� | D�� | 55�� |
| �շѷ�ʽ | ��ʹ�÷�/Ԫ | ��ʱ����ʱ��/h | ��ʱ��/��Ԫ/min�� |
| A | 7 | 25 | 0.6 |
| B | 10 | 50 | 0.8 |
��1����x��50ʱ���ֱ����yA��yB��x֮��ĺ�����ϵʽ��
��2����С��3�·��ϸ���վѧϰ��ʱ��Ϊ60Сʱ������ѡ�����ַ�ʽ����ѧϰ���㣿
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
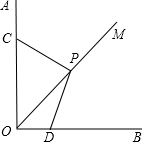 ��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��AOB=90�㣬OM�ǡ�AOB��ƽ���ߣ�PC��PD��PC=2��
��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��AOB=90�㣬OM�ǡ�AOB��ƽ���ߣ�PC��PD��PC=2��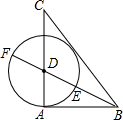 ��ͼ����֪��ABC�У�AB=3��AC=4��BC=5������ABC�Ľ�ƽ���߽�AC��D����DΪԲ�ģ�DAΪ�뾶��Բ�������߽��ڵ�E��F�������н��ۣ�
��ͼ����֪��ABC�У�AB=3��AC=4��BC=5������ABC�Ľ�ƽ���߽�AC��D����DΪԲ�ģ�DAΪ�뾶��Բ�������߽��ڵ�E��F�������н��ۣ�