题目内容
5.已知二次函数y=$-\frac{1}{2}$x2-2x+1,当x<-2时,y随x的增大而增大,当x>-2时,y随x的增大而减小.分析 二次函数y=$-\frac{1}{2}$x2-2x+1,抛物线开口向下,对称轴为x=-2,根据抛物线的性质得到在对称轴左侧y随x的增大而增大,右侧y随x的增大而减小,即可得到答案.
解答 解:二次函数y=$-\frac{1}{2}$x2-2x+1的对称轴x=-$\frac{b}{2a}$=-2,当x<-2时,y随x的增大而增大,当x>-2时,y随x的增大而减小.
故答案为:<-2;>-2.
点评 本题考查了二次函数的性质,掌握二次函数的开口方向、对称轴与增减性是解决问题的关键.

练习册系列答案
相关题目
20.抛物线y=-5(x+2)2-6的顶点坐标是( )
| A. | (2,-6) | B. | (-2,-6) | C. | (2,6) | D. | (-5,-6) |
14. 如图,四边形ABCD为⊙O的内接四边形,若∠BOD=90°,则∠BCD的大小为( )
如图,四边形ABCD为⊙O的内接四边形,若∠BOD=90°,则∠BCD的大小为( )
 如图,四边形ABCD为⊙O的内接四边形,若∠BOD=90°,则∠BCD的大小为( )
如图,四边形ABCD为⊙O的内接四边形,若∠BOD=90°,则∠BCD的大小为( )| A. | 90° | B. | 125° | C. | 135° | D. | 145° |
 如图,△ADF≌△BCE,∠B=30°,∠F=25°,BC=5cm,CD=1cm,DF=4cm,则AC=4cm.
如图,△ADF≌△BCE,∠B=30°,∠F=25°,BC=5cm,CD=1cm,DF=4cm,则AC=4cm.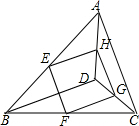 如图,E、F、G、H分别是边AB、BC、CD、DA的中点.当BD、AC满足什么条件时,四边形EFGH是正方形.
如图,E、F、G、H分别是边AB、BC、CD、DA的中点.当BD、AC满足什么条件时,四边形EFGH是正方形. 如图,D,E,F分别是三角形ABC各边的中点,AG是高,如果ED=5,那么GF的长为5.
如图,D,E,F分别是三角形ABC各边的中点,AG是高,如果ED=5,那么GF的长为5.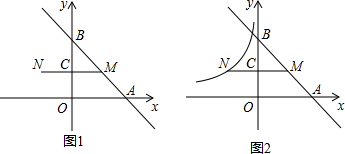
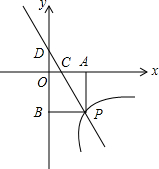 如图,一次函数y=kx+1的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴,y轴于点C,点D.且
如图,一次函数y=kx+1的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴,y轴于点C,点D.且