题目内容
9.谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注,人工智能完胜李世石,某教学网站开设了有关人工智能的课程并策划了A,B两种网上学习的月收费方式:| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 7 | 25 | 0.6 |
| B | 10 | 50 | 0.8 |
(1)当x≥50时,分别求出yA,yB与x之间的函数关系式;
(2)若小明3月份上该网站学习的时间为60小时,则他选择哪种方式上网学习合算?
分析 (1)根据收取费用=月使用费+超时单价×超过时间,可找出yA、yB关于x的函数关系式;
(2)将x=60分别代入yA、yB的表达式中得出y值进行比较,即可得出结论.
解答 解:(1)当x≥50时,yA与x之间的函数关系式为:
yA=7+(x-25)×0.6×60=36x-893,
当x≥50时,yB与x之间的函数关系式为:
yB=10+(x-50)×0.8×60=48x-2390.
(2)当x=60时,yA=36×60-893=1267,yB=48×60-2390=490,
∴yA>yB.
故选择B方式上网学习合算.
点评 本题考查了一次函数的应用,解题的关键是根据数量关系列出函数的表达式.本题属于基础题,难度很小,解决该题型题目时,寻找数量关系是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.抛物线y=-5(x+2)2-6的顶点坐标是( )
| A. | (2,-6) | B. | (-2,-6) | C. | (2,6) | D. | (-5,-6) |
14. 如图,四边形ABCD为⊙O的内接四边形,若∠BOD=90°,则∠BCD的大小为( )
如图,四边形ABCD为⊙O的内接四边形,若∠BOD=90°,则∠BCD的大小为( )
 如图,四边形ABCD为⊙O的内接四边形,若∠BOD=90°,则∠BCD的大小为( )
如图,四边形ABCD为⊙O的内接四边形,若∠BOD=90°,则∠BCD的大小为( )| A. | 90° | B. | 125° | C. | 135° | D. | 145° |
19.如图,将一个Rt△ABC形状的楔子从木桩的底端点P处沿水平方向打入木桩底下,使木桩向上运动,已知楔子斜面的倾斜角为18°,若楔子沿水平方向前移6cm(如箭头所示),则木桩上升了( )
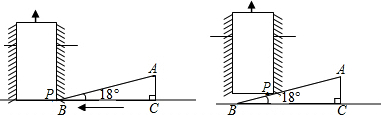
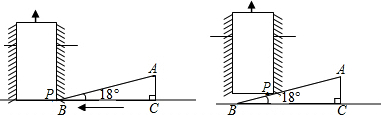
| A. | 6tan18°cm | B. | $\frac{6}{tan18°}$cm | C. | 6sin18°cm | D. | 6cos18°cm |
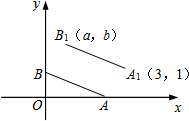 如图,A、B的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,A1、B1的坐标分别为(3,1)、(a,b),则a+b的值为3.
如图,A、B的坐标分别为(2,0)、(0,1),若将线段AB平移至A1B1,A1、B1的坐标分别为(3,1)、(a,b),则a+b的值为3. 如图,抛物线C1是二次函数y=x2-10x在第四象限的一段图象,它与x轴的交点是O、A1;将C1绕点A1旋转180°后得抛物线C2;它与x轴的另一交点为A2;再将抛物线C2绕A2点旋转180°后得抛物线C3,交x轴于点A3;如此反复进行下去…,若某段抛物线上有一点
如图,抛物线C1是二次函数y=x2-10x在第四象限的一段图象,它与x轴的交点是O、A1;将C1绕点A1旋转180°后得抛物线C2;它与x轴的另一交点为A2;再将抛物线C2绕A2点旋转180°后得抛物线C3,交x轴于点A3;如此反复进行下去…,若某段抛物线上有一点