题目内容
7.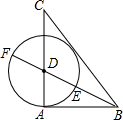 如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:
如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论:①△ABC是直角三角形;②⊙D与直线BC相切;③点E是线段BF的黄金分割点;④tan∠CDF=2.
其中正确的结论有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 由勾股定理的逆定理得出①正确;由角平分线的性质定理得出②正确;由全等三角形的性质得出MB=AB=3,证明△CDM∽△CBA,得出对应边成比例求出DM,根据勾股定理得出BD,求出EF2=BF•BE,得出③正确;由tan∠CDF=tan∠ADB=$\frac{AB}{AD}$=2,得出④正确,即可得出结论.
解答 解:∵32+42=52,
∴AB2+AC2=AB2,
∴△ABC是直角三角形,∠BAC=90°,①正确;
作DM⊥BC于M,如图所示: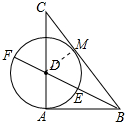
∵BD是∠ABC的平分线,
∴DM=DA,
∴⊙D与直线BC相切,
∴②正确;
∵∠BAC=∠DMC=90°,
在Rt△BDM和△BDA中,
$\left\{\begin{array}{l}{BD=BD}\\{DM=DA}\end{array}\right.$,
∴Rt△BDM≌△BDA(HL),
∴MB=AB=3,
∴CM=BC-MB=2,
∵∠C=∠C,
∴△CDM∽△CBA,
∴$\frac{DM}{AB}=\frac{CM}{AC}$,即$\frac{DM}{3}=\frac{2}{4}$,
解得:DM=$\frac{3}{2}$,
∴DF=DE=$\frac{3}{2}$,
∴BD=$\sqrt{A{B}^{2}++A{D}^{2}}$=$\sqrt{{3}^{2}+(\frac{3}{2})^{2}}$=$\frac{3\sqrt{5}}{2}$,
∴BE=BD-DE=$\frac{3\sqrt{5}}{2}$-$\frac{3}{2}$,BF=BD+DF=$\frac{3\sqrt{5}}{2}$+$\frac{3}{2}$,
∵EF2=9,BF•BE=($\frac{3\sqrt{5}}{2}$+$\frac{3}{2}$)($\frac{3\sqrt{5}}{2}$-$\frac{3}{2}$)=9,
∴EF2=BF•BE,
∴点E是线段BF的黄金分割点,③正确;
∵tan∠CDF=tan∠ADB=$\frac{AB}{AD}$=$\frac{3}{\frac{3}{2}}$=2,
∴④正确;
正确的有4个.
故选:A.
点评 本题考查了切线的判定、角平分线的性质、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理、三角函数;熟练掌握切线的判定,证明三角形全等和三角形相似是解决问题③的关键.

| A. | 15件 | B. | 30件 | C. | 150件 | D. | 1500件 |
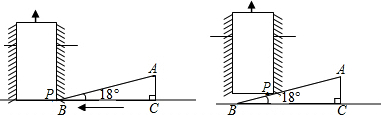
| A. | 6tan18°cm | B. | $\frac{6}{tan18°}$cm | C. | 6sin18°cm | D. | 6cos18°cm |
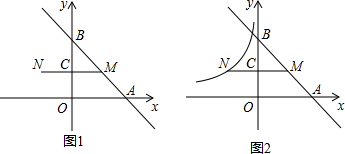
 如图,抛物线C1是二次函数y=x2-10x在第四象限的一段图象,它与x轴的交点是O、A1;将C1绕点A1旋转180°后得抛物线C2;它与x轴的另一交点为A2;再将抛物线C2绕A2点旋转180°后得抛物线C3,交x轴于点A3;如此反复进行下去…,若某段抛物线上有一点
如图,抛物线C1是二次函数y=x2-10x在第四象限的一段图象,它与x轴的交点是O、A1;将C1绕点A1旋转180°后得抛物线C2;它与x轴的另一交点为A2;再将抛物线C2绕A2点旋转180°后得抛物线C3,交x轴于点A3;如此反复进行下去…,若某段抛物线上有一点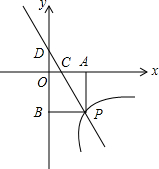 如图,一次函数y=kx+1的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴,y轴于点C,点D.且
如图,一次函数y=kx+1的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴,y轴于点C,点D.且 己知常数a(a是常数)满足下面两个条件:
己知常数a(a是常数)满足下面两个条件: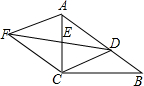 如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点(点D不与点A重合),点E是AC的中点,连结DE并延长至点F,使EF=DE,连结AF、CF.
如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点(点D不与点A重合),点E是AC的中点,连结DE并延长至点F,使EF=DE,连结AF、CF.