题目内容
8.为保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如表所示:| 港口 | 运费(元/吨) | |
| 甲库 | 乙库 | |
| A港 | 14 | 20 |
| B港 | 10 | 8 |
| 港口 | 运费(元/吨) | |
| 甲库 | 乙库 | |
| A港 | x | 100-x |
| B港 | 80-x | x-30 |
(3)求出最低费用,并说明费用最低时的调配方案.
分析 (1)设从甲仓库运送到A港口的物资为x吨,因为甲仓库一共有物资80吨,所以甲仓库运送到B港口的物资为(80-x)吨,因为A港口需要运送100吨物资,所以还要从乙仓库运送到A港口的物资为(100-x)吨,又因为乙仓库存有70吨物资,所以余下的物资:70-(100-x)=(x-30)吨,都要运到B港口;
(2)总费用=物资数量×运费,化成一般式即可,将甲、乙两仓库运往A、B两港口的物资数分别大于等于0,列不等式可求其x的取值范围;
(3)根据一次函数的增减性求得最小值,并写出调配方案.
解答 解:(1)设从甲仓库运送到A港口的物资为x吨,则甲仓库运送到B港口的物资为(80-x)吨,乙仓库运送到A港口的物资为(100-x)吨,乙仓库运送到B港口的物资为70-(100-x)=(x-30)吨,
故答案为:100-x,80-x,x-30;
(2)y=14x+10(80-x)+20(100-x)+8(x-30)=-8x+2560,
由题意得:$\left\{\begin{array}{l}{x≥0}\\{80-x≥0}\\{100-x≥0}\\{x-30≥0}\end{array}\right.$,
∴不等式的解集为:30≤x≤80,
∴总费用y(元)与x(箱)之间的函数关系式为:y=-8x+2560(30≤x≤80);
(3)∵-8<0,
∴y随x的增大而减小,
∴当x=80时,y有最小值,y=-8×80+2560=1920,
答:最低费用为1920元,此时的调配方案为:把甲仓库的全部运往A港口,再从乙仓库运20吨到A港口,乙仓库余下的50吨全部分运往B港口.
点评 本题是一次函数的应用,属于运输方案问题,此类问题比较麻烦,要认真理顺两仓库运往两地的物资数和运费;熟练掌握一次函数的增减性的性质,根据实际问题中的取值确定其最大值和最小值.

| A. | (5,4) | B. | (-5,-4) | C. | (-3,-4) | D. | (-5,4) |
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
| A. | x≠1 | B. | x≠-1 | C. | x≠1或x≠-1 | D. | x≠2 |
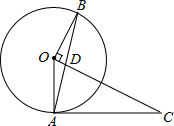 如图,在△OAC中,以点O为圆心、OA长为半径作⊙O,作OB⊥OC交⊙O于点B,连接AB交OC于点D,∠CAD=∠CDA.
如图,在△OAC中,以点O为圆心、OA长为半径作⊙O,作OB⊥OC交⊙O于点B,连接AB交OC于点D,∠CAD=∠CDA.