题目内容
20.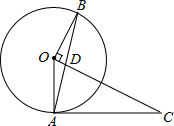 如图,在△OAC中,以点O为圆心、OA长为半径作⊙O,作OB⊥OC交⊙O于点B,连接AB交OC于点D,∠CAD=∠CDA.
如图,在△OAC中,以点O为圆心、OA长为半径作⊙O,作OB⊥OC交⊙O于点B,连接AB交OC于点D,∠CAD=∠CDA.(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OA=10,OD=2,求线段AC的长.
分析 (1)根据已知条件“∠CAD=∠CDA”、对顶角∠BDO=∠CDA可以推知∠BDO=∠CAD;然后根据等腰三角形OAB的两个底角相等、直角三角形的两个锐角互余的性质推知∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°,可得AC是⊙O的切线;
(2)根据“等角对等边”可以推知AC=DC,所以由图形知OC=OD+CD;然后利用(1)中切线的性质可以在Rt△OAC中,根据勾股定理来求AC的长度.
解答 解:(1)AC是⊙O的切线.
证明:∵点A,B在⊙O上,
∴OB=OA,
∴∠OBA=∠OAB,
∵∠CAD=∠CDA=∠BDO,
∴∠CAD+∠OAB=∠BDO+∠OBA,
∵BO⊥OC,
∴∠BDO+∠OBA=90°,
∴∠CAD+∠OAB=90°,
∴∠OAC=90°,即OA⊥AC,
又∵OA是⊙O的半经,
∴AC是⊙O的切线;
(2)设AC的长为x.
∵∠CAD=∠CDA,
∴CD的长为x.
由(1)知OA⊥AC,
∴在Rt△OAC中,OA2+AC2=OC2,
即102+x2=(2+x)2,
∴x=24,
即线段AC的长为24.
点评 此题考查了切线的性质与判定、勾股定理以及等腰三角形的性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
8.为保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如表所示:
(1)设从甲仓库运送到A港口的物资为x吨,用含x的式子填写下表:
(2)求总费用y(元)与x(箱)之间的函数关系式,并写出x的取值范围;
(3)求出最低费用,并说明费用最低时的调配方案.
| 港口 | 运费(元/吨) | |
| 甲库 | 乙库 | |
| A港 | 14 | 20 |
| B港 | 10 | 8 |
| 港口 | 运费(元/吨) | |
| 甲库 | 乙库 | |
| A港 | x | 100-x |
| B港 | 80-x | x-30 |
(3)求出最低费用,并说明费用最低时的调配方案.
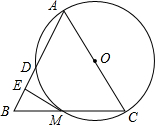 以△ABC的边AC为直径作⊙O,与AB、BC相交于点D、M,ME为⊙O的切线,ME⊥AB于E.
以△ABC的边AC为直径作⊙O,与AB、BC相交于点D、M,ME为⊙O的切线,ME⊥AB于E.