题目内容
16.已知二次函数y=-2x2+bx+c的图象经过点A(0,4)和B(1,-2).(1)求此抛物线的解析式;
(2)求此抛物线的对称轴和顶点坐标;
(3)设抛物线的顶点为C,试求△CAO的面积.
分析 (1)利用待定系数法把A(0,4)和B(1,-2)代入y=-2x2+bx+c中,可以解得b,c的值,从而求得函数关系式即可;
(2)利用配方法求出图象的对称轴和顶点坐标;
(3)由(2)可得顶点C的坐标,再根据三角形的面积公式即可求出△CAO的面积.
解答 解:(1)把A(0,4)和B(1,-2)代入y=-2x2+bx+c,
得:$\left\{\begin{array}{l}c=4\\-2×{1^2}+b+c=-2\end{array}\right.$,解得:$\left\{\begin{array}{l}b=-4\\ c=4\end{array}\right.$,
所以此抛物线的解析式为y=-2x2-4x+4;
(2)∵y=-2x2-4x+4
=-2(x2+2x)+4
=-2[(x+1)2-1]+4
=-2(x+1)2+6,
∴此抛物线的对称轴为直线x=-1,顶点坐标为(-1,6);
(3)由(2)知:顶点C(-1,6),
∵点A(0,4),∴OA=4,
∴S△CAO=$\frac{1}{2}$OA•|xc|=$\frac{1}{2}$×4×1=2,
即△CAO的面积为2.
点评 本题考查了用待定系数法求二次函数的解析式,二次函数解析式的三种形式,二次函数的性质以及三角形的面积,难度适中.正确求出函数的解析式是解题的关键.

练习册系列答案
相关题目
8.为保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如表所示:
(1)设从甲仓库运送到A港口的物资为x吨,用含x的式子填写下表:
(2)求总费用y(元)与x(箱)之间的函数关系式,并写出x的取值范围;
(3)求出最低费用,并说明费用最低时的调配方案.
| 港口 | 运费(元/吨) | |
| 甲库 | 乙库 | |
| A港 | 14 | 20 |
| B港 | 10 | 8 |
| 港口 | 运费(元/吨) | |
| 甲库 | 乙库 | |
| A港 | x | 100-x |
| B港 | 80-x | x-30 |
(3)求出最低费用,并说明费用最低时的调配方案.
6.某自行车厂为了赶速度,一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产辆与计划量相比有出入,表是某周的生产情况(超产为正,减产为负):
(1)根据记录可知第一天生产多少辆?
(2)产量最多的一天比产量最少的一天多生产多少辆?
(3)赶进度期间该厂实行计件工资加浮动工资制度,即:每生产一辆车的工资为60元,超过计划完成任务每辆车则在原来60元工资上在奖励15元;比计划每少生产一辆则在应得的总工资上扣发15元(工资按日统计,每周汇总一次),求该厂工人这一周的工资总额是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
(2)产量最多的一天比产量最少的一天多生产多少辆?
(3)赶进度期间该厂实行计件工资加浮动工资制度,即:每生产一辆车的工资为60元,超过计划完成任务每辆车则在原来60元工资上在奖励15元;比计划每少生产一辆则在应得的总工资上扣发15元(工资按日统计,每周汇总一次),求该厂工人这一周的工资总额是多少?
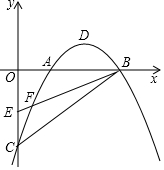 已知:如图,在平面直角坐标系中,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,-1),该抛物线与BE交于另一点F,连接BC.
已知:如图,在平面直角坐标系中,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,-1),该抛物线与BE交于另一点F,连接BC.