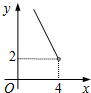题目内容
8.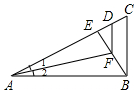 如图,Rt△ABC中,∠ABC=90°,AB⊥AC,∠1=∠2,AD=AB,则( )
如图,Rt△ABC中,∠ABC=90°,AB⊥AC,∠1=∠2,AD=AB,则( )| A. | ∠1=∠EFD | B. | BE=CE | C. | BF-DE=CD | D. | DF∥BC |
分析 由AD=AB,∠1=∠2,AF为公共边,利用SAS可得出三角形AFD与三角形AFB全等,利用全等三角形的对应角相等得到∠ADF=∠ABE,再利用同角的余角相等得到一对同位角相等,利用同位角相等两直线平行即可得出FD与BC平行,得证.
解答 解:在△ADF和△ABF中,
$\left\{\begin{array}{l}{AD=AB}\\{∠2=∠1}\\{AF=AF}\end{array}\right.$,
∴△ADF≌△ABF(SAS),
∴∠ADF=∠ABE,
∵∠C+∠BAC=90°,∠ABE+∠BAC=90°,
∴∠C=∠ABE=∠ADF,
∴DF∥BC.
故选D.
点评 此题考查了全等三角形的判定与性质,以及平行线的判定,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.怎样测量某种食用油沸腾时的温度?因为油的沸点温度很高,用普通温度计很难直接测量,于是,小明设计了一个实验:取适量食用油在锅里用煤气灶开小火进行均匀加热,每隔5秒钟用普通温度计(测量范围在0℃-100℃之间)测量一次油温,结果如表:
而且小明发现50秒后该食用油沸腾.根据上述分析,你认为下面对该食用油沸点温度估计较为可靠的是( )
| 时间(s) | 0 | 5 | 10 | 15 |
| 食用油温度(℃) | 20 | 35 | 50 | 65 |
| A. | 85℃ | B. | 120℃ | C. | 150℃ | D. | 170℃ |
3.平行四边形ABCD的四个顶点都在圆O上,那么四边形ABCD一定是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 以上都不对 |
13.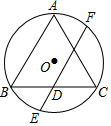 如图,等边△ABC内接于⊙O,点D是BC的中点,过点D作AB的平行线交⊙O于点E,F,则$\frac{EF}{BC}$的值是( )
如图,等边△ABC内接于⊙O,点D是BC的中点,过点D作AB的平行线交⊙O于点E,F,则$\frac{EF}{BC}$的值是( )
 如图,等边△ABC内接于⊙O,点D是BC的中点,过点D作AB的平行线交⊙O于点E,F,则$\frac{EF}{BC}$的值是( )
如图,等边△ABC内接于⊙O,点D是BC的中点,过点D作AB的平行线交⊙O于点E,F,则$\frac{EF}{BC}$的值是( )| A. | 2 | B. | 1.5 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
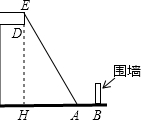 小明的爸爸用10m长的梯子一头支在地面的A处,一头正巧搁在屋檐顶部的E处,屋檐板ED为0.9m,A到围墙底部B的距离为1m,E点的高度EH=8m,小明建议爸爸:“太危险,梯子滑下去就会出事”,爸爸回答:“没事,梯子左右不滑,上下滑有围墙挡着呢”,你认为小明爸爸说得对吗?请你阐述判断的根据.
小明的爸爸用10m长的梯子一头支在地面的A处,一头正巧搁在屋檐顶部的E处,屋檐板ED为0.9m,A到围墙底部B的距离为1m,E点的高度EH=8m,小明建议爸爸:“太危险,梯子滑下去就会出事”,爸爸回答:“没事,梯子左右不滑,上下滑有围墙挡着呢”,你认为小明爸爸说得对吗?请你阐述判断的根据. 如图,已知直线l及其两侧两点A、B.
如图,已知直线l及其两侧两点A、B. 如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=$\frac{k}{x}$(x<0)的图象过点P,则k的值为( )
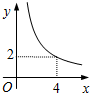
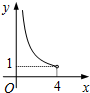
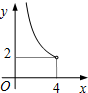
如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=$\frac{k}{x}$(x<0)的图象过点P,则k的值为( )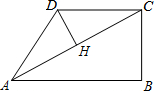 在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )