题目内容
16. 如图,已知直线l及其两侧两点A、B.
如图,已知直线l及其两侧两点A、B.(1)在直线l上求一点Q,使QA、QB与l的夹角相等;
(2)在直线l上求一点S,使|SA-SB|最大.
分析 (1)如图1中,作点A关于直线l的对称点A′,连接BA′交直线l于Q,点Q即为所求的点.
(2)如图2中,连接BA,延长BA交直线l于S,点S即为所求的点.
解答 解:(1)如图1中,作点A关于直线l的对称点A′,连接BA′交直线l于Q,点Q即为所求的点.
理由:∵A、A′关于EF对称,
∴∠AQF=∠A′QF,
∵∠A′QF=∠BQE,
∴∠BQE=∠AQF,
∴点Q即为所求.
(2)如图2中,连接BA,延长BA交直线l于S,点S即为所求的点.
理由:∵|SA-SB|≤AB,
∴当B、A、S共线时,
|SA-SB|的值最大,
∴点S即为所求.
点评 本题考查轴对称、三角形的三边关系等知识,解题的关键是学会利用对称解决问题,掌握利用三角形的三边关系解决最大值问题,属于参考常考题型.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
8.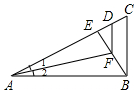 如图,Rt△ABC中,∠ABC=90°,AB⊥AC,∠1=∠2,AD=AB,则( )
如图,Rt△ABC中,∠ABC=90°,AB⊥AC,∠1=∠2,AD=AB,则( )
 如图,Rt△ABC中,∠ABC=90°,AB⊥AC,∠1=∠2,AD=AB,则( )
如图,Rt△ABC中,∠ABC=90°,AB⊥AC,∠1=∠2,AD=AB,则( )| A. | ∠1=∠EFD | B. | BE=CE | C. | BF-DE=CD | D. | DF∥BC |
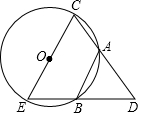 如图,CE是⊙O的直径,AB、AC是⊙O的两条弦,且AB=AC,延长CA、EB交于点D,问AD=AC吗?为什么?
如图,CE是⊙O的直径,AB、AC是⊙O的两条弦,且AB=AC,延长CA、EB交于点D,问AD=AC吗?为什么?