题目内容
如图：AC⊥BC，BD⊥AD，BD与AC交于E，AD=BC，求证：AE=BE．考点：全等三角形的判定与性质
专题：证明题
分析：由已知两垂直得到一对直角相等，在直角三角形ADB与直角三角形BCA中，利用HL得到两三角形全等，利用全等三角形的对应角相等得到一对角相等，利用等角对等边即可得证．
解答：证明：∵AC⊥BC，BD⊥AD，
∴∠C=∠D=90°，
在Rt△ADB和Rt△BCA中，
，
∴Rt△ADB≌Rt△BCA（HL），
∴∠ABD=∠CAB，
则AE=BE．
∴∠C=∠D=90°，
在Rt△ADB和Rt△BCA中，
|
∴Rt△ADB≌Rt△BCA（HL），
∴∠ABD=∠CAB，
则AE=BE．
点评：此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．
练习册系列答案
优学名师名题系列答案
相关题目
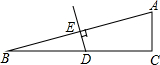如图所示，在△ABC中，∠C=90°，∠B=15°，AB的垂直平分线交AB于E，交BC于D，DB=10，那么AC=（ ）| A、5 | B、10 | C、15 | D、20 |
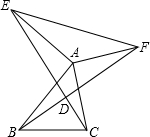已知：AB=AE，AB⊥AE，AC=AF，AC⊥AF．
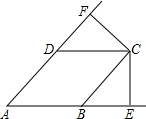如图，四边形ABCD是菱形，CE⊥AB交AB延长线于E，CF⊥AD交AD延长线于F，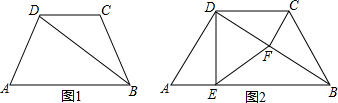
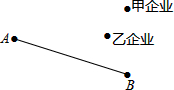在国家“西电东送”工程中，为发展地方经济，促进甲、乙两大型企业发展，又为方便A，B两村群众，在如图所示的地理位置中，准备修一个变电站P，使变电站到A，B两村的距离相等，又要到甲、乙两企业的距离最短，请在图中作出P点的位置．（保留作图痕迹）
画出函数y=-2x+2的图象，观察图象并回答下列问题．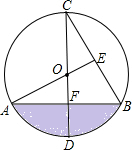
如图，CD为⊙O的直径，CD⊥AB于点F，AO⊥BC于点E，AO=2．