题目内容
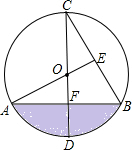 如图,CD为⊙O的直径,CD⊥AB于点F,AO⊥BC于点E,AO=2.
如图,CD为⊙O的直径,CD⊥AB于点F,AO⊥BC于点E,AO=2.(1)求∠AOD的度数;
(2)求阴影部分的面积.
考点:垂径定理,扇形面积的计算
专题:
分析:(1)先根据垂径定理得出AF=BF,
=
,再由圆周角定理得出∠COE=2∠C,根据AE⊥BC即可得出结论;
(2)连结OB,根据垂径定理及圆周角定理得出∠AOB=2∠AOD=120°,OF=
AO=1,AB=2AF=2,再由S阴影=S扇形OAB-S△OAB即可得出结论.
 |
| AD |
 |
| BD |
(2)连结OB,根据垂径定理及圆周角定理得出∠AOB=2∠AOD=120°,OF=
| 1 |
| 2 |
解答: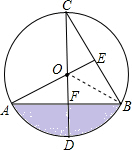 解:(1)∵CD为直径,CD⊥AB,
解:(1)∵CD为直径,CD⊥AB,
∵AF=BF,
=
,
∴∠AOD=
=
=2∠C,
∵∠COE=∠AOF,
∴∠COE=2∠C.
∵AE⊥BC,
∴∠C=90°×
=30°,∠AOD=60°;
(2)连结OB,
∵∠AOB=2∠AOD=120°,OF=
AO=1,AB=2AF=2
∴S扇形OAB=
=
π,
S△OAB=
AB•OF=
×2
×1=
,
∴S△OAB=
π-
.
 解:(1)∵CD为直径,CD⊥AB,
解:(1)∵CD为直径,CD⊥AB,∵AF=BF,
 |
| AD |
 |
| BD |
∴∠AOD=
 |
| AD |
 |
| BD |
∵∠COE=∠AOF,
∴∠COE=2∠C.
∵AE⊥BC,
∴∠C=90°×
| 1 |
| 3 |
(2)连结OB,
∵∠AOB=2∠AOD=120°,OF=
| 1 |
| 2 |
| 3 |
∴S扇形OAB=
| 120π×22 |
| 360 |
| 4 |
| 3 |
S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S△OAB=
| 4 |
| 3 |
| 3 |
点评:本题考查的是垂径定理,熟知垂径定理‘圆周角定理及扇形的面积公式是解答此题的关键.

练习册系列答案
相关题目
当-2<x<2时,下列函数:①y=2x;②y=-2+
x;③y=-
;④y=x2+6x+8,函数值y随自变量x增大而增大的有( )
| 1 |
| 3 |
| 6 |
| x |
| A、①② | B、①②③ |
| C、①②④ | D、①②③④ |
 如图:AC⊥BC,BD⊥AD,BD与AC交于E,AD=BC,求证:AE=BE.
如图:AC⊥BC,BD⊥AD,BD与AC交于E,AD=BC,求证:AE=BE. 如图,△ABC中,∠A=90°,∠C的平分线交AB于D,若∠DCB=2∠B,求∠ADC的度数.
如图,△ABC中,∠A=90°,∠C的平分线交AB于D,若∠DCB=2∠B,求∠ADC的度数.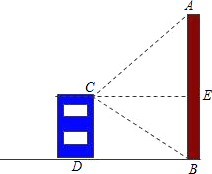 在旧城改造中,要拆除一烟囱AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在从离B点21米远的建筑物CD顶端C测得A点的仰角为45°,到B点的俯角为30°,问离B点30米远的保护文物是否在危险区内?(
在旧城改造中,要拆除一烟囱AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在从离B点21米远的建筑物CD顶端C测得A点的仰角为45°,到B点的俯角为30°,问离B点30米远的保护文物是否在危险区内?(