题目内容
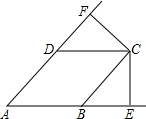如图，四边形ABCD是菱形，CE⊥AB交AB延长线于E，CF⊥AD交AD延长线于F，求证：CE=CF．
考点：菱形的性质,角平分线的性质
专题：证明题
分析：连接AC，根据菱形的性质可得AC平分∠DAE，再根据角平分线的性质可得CE=FC．
解答：
证明：连接AC，
∵四边形ABCD是菱形，
∴AC平分∠DAE，
∵CE⊥AB，CF⊥AD，
∴CE=FC．
证明：连接AC，∵四边形ABCD是菱形，
∴AC平分∠DAE，
∵CE⊥AB，CF⊥AD，
∴CE=FC．
点评：此题主要考查了菱形的性质，以及角平分线的性质，关键是掌握菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；角平分线的性质：角的平分线上的点到角的两边的距离相等．
练习册系列答案
相关题目
若|a|=5，则a的值是（ ）
| A、-5 | B、5 | C、±5 | D、都不是 |
当-2＜x＜2时，下列函数：①y=2x；②y=-2+
x；③y=-
；④y=x2+6x+8，函数值y随自变量x增大而增大的有（ ）
| 1 |
| 3 |
| 6 |
| x |
| A、①② | B、①②③ |
| C、①②④ | D、①②③④ |
如图，点P是∠AOB的边OB上一点，读句画图，并回答问题
如图，已知：DE∥BC，CD是∠ACB的平分线，∠A=60°，∠ACB=50°，求∠EDC和∠BDC的度数．
如图：AC⊥BC，BD⊥AD，BD与AC交于E，AD=BC，求证：AE=BE．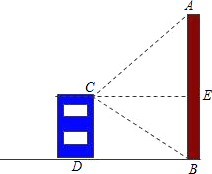
在旧城改造中，要拆除一烟囱AB，在地面上事先划定以B为圆心，半径与AB等长的圆形危险区，现在从离B点21米远的建筑物CD顶端C测得A点的仰角为45°，到B点的俯角为30°，问离B点30米远的保护文物是否在危险区内？（