题目内容
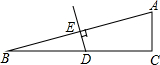 如图所示,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于E,交BC于D,DB=10,那么AC=( )
如图所示,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交AB于E,交BC于D,DB=10,那么AC=( )| A、5 | B、10 | C、15 | D、20 |
考点:线段垂直平分线的性质,含30度角的直角三角形
专题:
分析:连接AD,根据线段垂直平分线上的点到两端点的距离相等可得AD=BD,根据等边对等角可得∠BAD=∠B,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ADC,然后利用直角三角形30°角所对的直角边等于斜边的一半可得AC=
AD.
| 1 |
| 2 |
解答: 解:如图,连接AD,
解:如图,连接AD,
∵DE是AB的垂直平分线,
∴AD=BD,
∴∠BAD=∠B=15°,
在△ABD中,∠ADC=∠B+∠BAD=15°+15°=30°,
在△ACD中,AC=
AD=
×10=5.
故选A.
 解:如图,连接AD,
解:如图,连接AD,∵DE是AB的垂直平分线,
∴AD=BD,
∴∠BAD=∠B=15°,
在△ABD中,∠ADC=∠B+∠BAD=15°+15°=30°,
在△ACD中,AC=
| 1 |
| 2 |
| 1 |
| 2 |
故选A.
点评:本题考查了线段垂直平分线上的点到两端点的距离相等的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记各性质是解题的关键.

练习册系列答案
相关题目
下列四个点,在反比例函数y=
的图象上的是( )
| 6 |
| x |
| A、(1,-6) |
| B、(2,4) |
| C、(3,-2) |
| D、(-6,-1) |
若|a|=5,则a的值是( )
| A、-5 | B、5 | C、±5 | D、都不是 |
下列二次根式中,最简二次根式是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
多项式6a-2a3x3y-8+4x5的次数为( )
| A、5 | B、6 | C、7 | D、8 |
若分式方程
-
=-
有增根,则增根是( )
| 3 |
| x+1 |
| 2 |
| x |
| 3 |
| x2+x |
| A、x=0 | B、x=0和x=-1 |
| C、x=-1 | D、无法确定 |
当-2<x<2时,下列函数:①y=2x;②y=-2+
x;③y=-
;④y=x2+6x+8,函数值y随自变量x增大而增大的有( )
| 1 |
| 3 |
| 6 |
| x |
| A、①② | B、①②③ |
| C、①②④ | D、①②③④ |
 如图:AC⊥BC,BD⊥AD,BD与AC交于E,AD=BC,求证:AE=BE.
如图:AC⊥BC,BD⊥AD,BD与AC交于E,AD=BC,求证:AE=BE.