题目内容
1. 如图,在△ABC中,如果AB=AC,两条角平分线BD、CE相交于点O,那么OB与OC相等吗?为什么?
如图,在△ABC中,如果AB=AC,两条角平分线BD、CE相交于点O,那么OB与OC相等吗?为什么?
分析 要证OB=OC,只要∠DBC=∠ECB即可,可利用等腰三角形的定义、性质以及角平分线的定义进行证明.
解答 解:OB=OC,
证明如下:
∵AB=AC
∴∠ABC=∠ACB
又∵BD、CE是角平分线
∴∠DBC=∠ECB
∴OB=OC.
点评 本题考查了等腰三角形等边对等角及等角对等边的性质及角平分线的性质;角平分线性质的利用是正确解答本题的关键.

练习册系列答案
相关题目
12. 如图,在四边形ABCD中,∠A=140°,∠D=90°,OB平分∠ABC,OC平分∠BCD,则∠BOC=( )
如图,在四边形ABCD中,∠A=140°,∠D=90°,OB平分∠ABC,OC平分∠BCD,则∠BOC=( )
 如图,在四边形ABCD中,∠A=140°,∠D=90°,OB平分∠ABC,OC平分∠BCD,则∠BOC=( )
如图,在四边形ABCD中,∠A=140°,∠D=90°,OB平分∠ABC,OC平分∠BCD,则∠BOC=( )| A. | 105° | B. | 115° | C. | 125° | D. | 135° |
13.某乡镇企业生产部有技术工人15人,为了合理制定产品的每月定额,统计了15人月的加工零件个数:
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如负责人把每位工人的月加工零件数定为260(件),你认为这个定额是否合理,为什么?
| 每人加工件数 | 540 | 450 | 300 | 240 | 210 | 120 |
| 人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(2)假如负责人把每位工人的月加工零件数定为260(件),你认为这个定额是否合理,为什么?
10. 如图所示的几何体的主视图是( )
如图所示的几何体的主视图是( )
 如图所示的几何体的主视图是( )
如图所示的几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
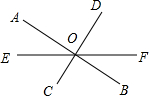 如图,直线AB与CD相交于点O,若∠AOD=70°,∠BOE-∠BOC=50°,求∠DOE的度数.
如图,直线AB与CD相交于点O,若∠AOD=70°,∠BOE-∠BOC=50°,求∠DOE的度数.