题目内容
3. 如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.(1)实验与探究
由图观察易知点A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5),E(-1,-4)关于直线l的对称点B′、C′,E′的位置,并写出它们的坐标:B′(3,5)、C′(5,-2),E′(-4,-1);
(2)归纳与发现:
结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为(b,a)(不必证明);
(3)运用与拓广:
已知两点D(1,-3)、B(5,3),试在直线l上确定一点Q,使点Q到D、B两点的距离之和最小,并求出Q点坐标.
分析 (1)根据对称的性质作出对称点即可,然后写出坐标.
(2)观察(1)中结论得出结论即可.
(3)连接DB′交直线l于Q,此时DQ+BQ最小.求出直线DB′的解析式,解方程组即可求出点Q坐标.
解答 解:(1)点B(5,3)、C(-2,5),E(-1,-4)关于直线l的对称点B′、C′,E′的位置,如图所示,
由图象可知B′(3,5),C′(5,-2),E′(-4,-1).
(2)由(1)可知坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为(b,a).
(3)连接DB′交直线l于Q,此时DQ+BQ最小.
设直线DB′的解析式为y=kx+b,则$\left\{\begin{array}{l}{k+b=-3}\\{3k+b=5}\end{array}\right.$解得$\left\{\begin{array}{l}{k=4}\\{b=-7}\end{array}\right.$,
∴直线DB′的解析式为y=4x-7,
由$\left\{\begin{array}{l}{y=4x-7}\\{y=x}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{7}{3}}\\{y=\frac{7}{3}}\end{array}\right.$,
∴点Q坐标($\frac{7}{3}$,$\frac{7}{3}$).
点评 本题考查轴对称-最短问题、坐标与图形的性质等知识,解题的关键是学会正确画出图形,学会利用对称解决最短问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15. 如图,直角三角形的三边长分为a、b、c,下列各式正确的是( )
如图,直角三角形的三边长分为a、b、c,下列各式正确的是( )
 如图,直角三角形的三边长分为a、b、c,下列各式正确的是( )
如图,直角三角形的三边长分为a、b、c,下列各式正确的是( )| A. | a2+b2=c2 | B. | b2+c2=a2 | C. | c2+a2=b2 | D. | 以上都不对 |
 如图,A、B两点分别位于山脚的两端,小明想测量A、B两点间的距离,于是想了个主意:先在地上取一个可以直接达到A、B两点的点C,找到AC、BC的中点D、E,并且测出DE的长为15m,则A、B两点间的距离为30m.
如图,A、B两点分别位于山脚的两端,小明想测量A、B两点间的距离,于是想了个主意:先在地上取一个可以直接达到A、B两点的点C,找到AC、BC的中点D、E,并且测出DE的长为15m,则A、B两点间的距离为30m.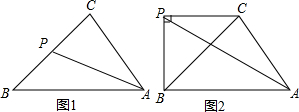
 如图是一套住房的平面图,尺寸如图所.
如图是一套住房的平面图,尺寸如图所. 已知:如图,AD=BC,AC=BD,试证明:∠CAD=∠DBC.
已知:如图,AD=BC,AC=BD,试证明:∠CAD=∠DBC.